Building a RS with one method and then reversing it

General
1

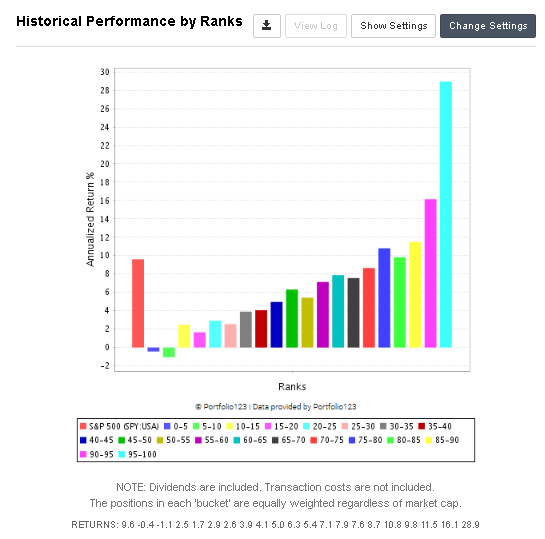
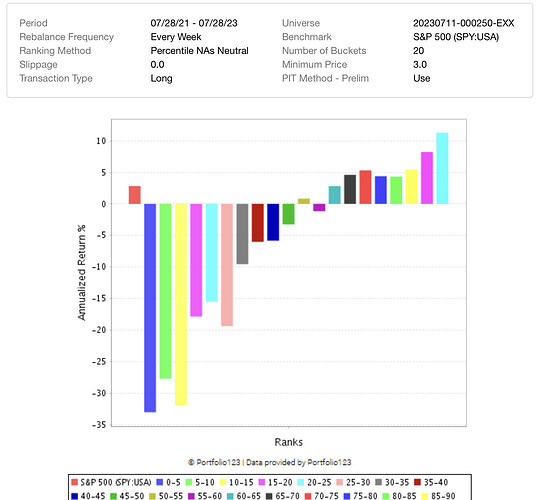
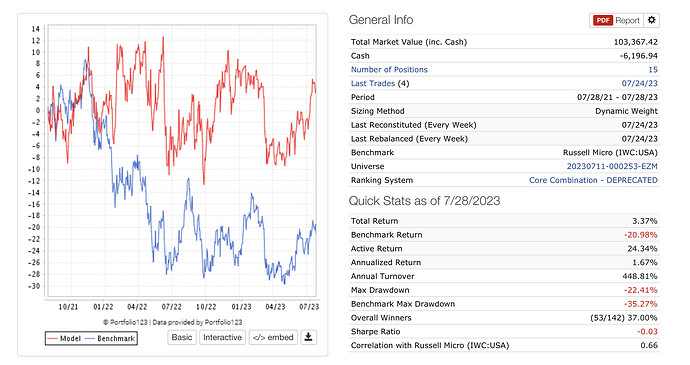
I’m still working on this time-consuming and annoying optimisation process of ranking systems, just to learn of the prosess on how to best put RS together.

I did a test with 150 nodes, which I believe in, where I started the RS without any composite nodes and just the Small Cap Focus RS. Then I added one and one of my own nodes. And I ran the simulator on the full US Canada universe (with a liquidity rule). If it did better, I kept the node, and if it did worse, I set it to 0%. I ran it with the full history, and with 25 stocks. And each new node should at least weigh more than 1%.

Then I did the opposite. I added all 150 to the 39 that are already in the Focus RS. Here I equally weighted each of the 150, so that, in total, that part of the RS did not have more than 50%, and each node got around 0.35%. Then I set each to 0%, ran the simulator, and kept only the ones that made the performance better.

And Yes, I know, this is overfitting. And the performance difference could be something of a coincidence.

The surprising thing is still that the last method did far better than the first one. Not just in total performance but also in the performance increase through the process. Anyone who has a good explanation of why the difference?

It seems that a large part of building a RS is not only finding nodes that make sense but also understanding how factors interact with each other.

3

Whycliffes, I probably would not trust either of those methods to find good factors or ranking systems. The first method will likely be coincidental, as you pointed out. The second method introduces a lot of noise with all the sub 1% weights. From my experience, noise seems to work great on backtests and terrible out of sample. I have yet to find a reliable way to test individual factors.

Tony

4

In the first example, if a factor you added improved the result, did you keep it and then test another factor? Or did you remove it and test another factor against the base RS? If you kept it and continued adding factors, I’d think the order you tested them in would determine what you ended up with due to the way they are interacting. For instance, you could have one that tests poorly and is thrown out, but if you’d included it further on in the test after more factors had been added it might improve the overall result.

5

Not surprising the second method did better. It is a manual approximation of what is behind the random forest method – examine everything and discard what doesn’t contribute positively.

Cheers,
Rich

6

Whycliffes,

What you are doing has similarities to Forward and Backward Stepwise Regression, I think. You might google that.

Here is one resource that has an opinion as to when backward regression is better (i.e., starting with all of the variables and removing one at at time).

Source: Understand Forward and Backward Stepwise Regression

I think it has a simple rule of thumb and an explanation for what you are noticing. I did not do a thorough search. You might finish searching this topic if you are interested (or ask ChatGPT which agrees with backward stepwise regression’s advantage with regard to collinearly concerns).

And simply put you are going to have a little collinearity with 150 nodes. You can take that as a simple statement of fact

I might add that Duckruck has tried to present other methods to address collinearity to the forum. I leave it to him to repeat those if he wishes. But from the link:

"This is especially important in case of collinearity (when variables in a model are correlated which each other) because backward stepwise may be forced to keep them all in the model unlike forward selection where none of them might be entered [see Mantel].

BOTTOM LINE:

Unless the number of candidate variables > sample size (or number of events), use a backward stepwise approach."

You might confirm this if you want but that last rule of thumb may be what you need to know,

P123 says they will be providing regressions with their AI/ML, I think. I wonder if P123 will include automated backward stepwise recession. You are right, I believe. It is a good idea

Jim

7

The collinearity issue is interesting. Must collinear factors be discarded/mininized? Instead, can those factors be group within a composite group? Given that data coverage can be spotty, that approach would seem to offer more resiliency.

8

I have a few questions. When you added the 150 factors to the 39, was the immediate performance better or worse? How are you assessing performance? You said the “simulator”. If you are talking about the portfolio simulator then you should switch to the ranking system performance page and look for an upward slope in ranking buckets. You also want to consider where the N/As are placed. If they are given a zero rank then the lower buckets will be inconsequential. And oh yeah welcome to the dark side (optimization).

9

Walter,

As an aside. You can read things that say for predictive models collinearity is not important. But they are referring to i.i.d. (independent and identically distributed) variables. And even then this is debated.

IMHO, you can just ignore that completely for the stock market which is non-stationary and definitely not i.i.d. data. Call it BS and move on. Collinearity does matter.

PCA (principle component analysis) first presented by Duckruck is possibly the most commonly cited method to accomplish what you suggest: "factors be grouped within a composite group? "

More simply: Yes. That can be done with PCA as Durckruck has already said.

Also regularization is very helpful. Again Duckruck tried to present that in a thread with Lasso regression as a method;. He presented this in a post and suggested it could be paired within the linear methods P123 uses.

Oh and he mentioned Elastic net regression.

It is fun rediscovering things thing that are already well-understood like Whycliffes has done here while ignoring Duckruck’s comments as being too complex, but I think that is not really the best thing for P123 if it wants to market to machine learners.

Regression is the simplest machine learning model. Full stop. We are going to have neural nets at P123? Who is going to explain that in the forum? Even the most advanced will have questions about the batch size used and want to understand how early stopping is implemented (if it is).

Monotonic constraints for XGBoost? Subsample columns? How about XGBoost’s regularization method? Oh yea, early stopping is an important issue with XGBoost too.

Out-of-bag validation for random forests?

Sticking with simple regressions for now, ChatGPT has a answer that supports everything Duckruck has said (and a little more):

"Certainly! Collinearity (or multicollinearity in multiple regression contexts) refers to a situation in which two or more predictor variables in a regression model are highly correlated. When collinearity is present, it can inflate the variance of the regression coefficients, making them unstable and harder to interpret. Here are some ways to address collinearity in regressions:

  1. Variance Inflation Factor (VIF):

    • VIF measures the inflation in the variances of the parameter estimates due to collinear predictors.
    • A VIF value of 1 indicates no collinearity, whereas a value greater than 1 suggests increasing collinearity. A common threshold is a VIF > 10, which indicates high collinearity.
    • By examining VIFs, you can detect which variables are contributing to multicollinearity and consider removing the ones with very high VIF values.

  2. Correlation Matrix:

    • Before performing regression, compute the correlation matrix for predictors.
    • If two or more variables have a high correlation (e.g., above 0.8 or below -0.8), consider this a sign of collinearity.

  3. Principal Component Analysis (PCA)

    • PCA is a dimensionality reduction technique.
    • Instead of using original correlated predictors, you use uncorrelated principal components generated by PCA as predictors in the regression.

  4. Remove/Combine Predictors

    • If two or more predictors are highly correlated, consider removing one or combining them into a single predictor.
    • For instance, if two measurements capture similar information, use an average or a principal component of them.

  5. Regularization:

    • Techniques like Ridge and Lasso regression can help mitigate the effects of collinearity.
    • Ridge regression adds a penalty to the size of coefficients, which can help in the presence of collinearity. Lasso regression can force some coefficients to be exactly zero, effectively performing variable selection.

  6. Increase Sample Size:

    • If feasible, adding more data points can sometimes help mitigate the effects of collinearity.

  7. Centering Variables:

    • Subtracting the mean of a predictor variable from each data point can help reduce multicollinearity, especially when interaction terms are involved.

  8. Expert Judgment:

    • Use domain knowledge to decide which variables to keep or remove.
    • If one variable is clearly more theoretically relevant than another, prioritize that one.

  9. Drop Interaction or Polynomial Terms:

    • Interaction and polynomial terms can exacerbate collinearity, especially if the original predictors are already correlated.
    • Consider omitting such terms or using them judiciously.

  10. Use Hierarchical Regression:

  • In hierarchical regression, predictors are entered into the regression equation in stages based on theoretical or logical considerations. This can help you understand the effect of each block of variables and potentially manage multicollinearity.

Addressing collinearity is essential for creating reliable and interpretable regression models. When handling collinearity, it’s vital to be guided by both statistical evidence and domain knowledge to make informed decisions."

Jim

1 Like
10

Thanks Jim, this is what I had in mind, but “averaging” would be done when the ranking system combines two (or more) factor within a composite group.

The rest of the info is very interesting to me. More study time is needed.

Thanks.

11

Yes, the NA is set to neuteral. I understand that this, in most cases, will give better performance. But is it also a problem? Is it simpler to overoptimize?

And yes, when adding the 150 nodes, it immediately gave better performance.

Here are the differences:

Original Smallcap:

image
image582×616 20.5 KB

Here with the added nodes:

image
image545×539 19.2 KB

12

I agree.

13

What do you think of the core system? That has 99 nodes, end several with less than 1%?

14

Core Combination? It actually has 66 factors. 33 nodes are composite containers. How has it done out of sample?

Tony

15

Im not sure, when was it published?

16

The reference was to Core: Combination;
https://www.portfolio123.com/app/ranking-system/408565

What are you referring to?

17

The samme: Core: Combination;

18

Great! So there are two dates attached to that ranker; Created, Updated. Both are fairly current. So any oos results are short lived.

19

Take a look at the “deprecated” version. Its been around a while.
With my universe for the past two years. And quite a bit better than the SP500.

IMG_1772
IMG_17721377×1233 135 KB

And with all my rules, its not so good. Try your rules.

IMG_1773
IMG_17731997×1059 314 KB

Tony

20

Whycliffes and Tony (Walter too),

I like what you guys are doing. I emphasize collinearity in this thread only because it was an answer to a question.

Have any of you tried optimizing the core factors by whatever method any of you may prefer up until its release? Just the factors in the ranking system. Preferably sticking with an algorithm you can write down (but would not have to share).

Preferably for this to work the selection of factors would be purely based on an algorithm and not “earnings estimate have work for me for the last 5 years so I will select that factor.” That would be look-ahead bias. My selection method is purely based on an algorithm. But not 100% without some look-ahead bias. I would be the first person to stress this. But all factors were selected or excluded by an algorithm that could be written down.

Some of this is hard to do. For myself as an example, I started with all of the core factors and a few of my own. And trained a system up to certain date. And tested it after that date. So the factors were fixed.I did make some minor changes since I did this" holdout test set" so not perfectly done. Also, I have added factors–based on the algorithm–without a new cross-validation. So I cannot say my entire system is cross-validated.

But much of this initial holdout test set was after the Core Ranking system had been developed and the training portion was before the system war released.

In the future with P123 AI/ML and fast computers, one would select a set of factors and run Yuval’s method (if public), Whychliffe’s method (if public), Walter’s method (if public), mine will not be public, regression, support vector machines, random forest, XGBoost, neural net etc. Train the method up to a certain date and then test after that date.

You could add your own opinions to the decision. Not even test your best guess of my method or Jane Doe’s if you have a strong opinion. But if your opinions are faily neutral on the other methods then just pick the method with the best out-of-sample results.

Edit: I initially made this a competition and I still think it would be a good idea if it did not get too competitive. It would be better than competing backtests which give you no idea as to how much overfitting there is.

You would probably want to test your algorithm with different sets of factors. You could even randomly select factors from a large population of factors multiple times to get the best algorithm.

Hmmm….after you have the best model, maybe model-average models that are built from randomly selected factors. But then that would be doing something like what is done with a random forest and would begin to look like machine learning. :dizzy_face:

Jim