Imagine if you could predict with 60% certainty whether the market will go up or down tomorrow — theoretically, this should make you a billionaire in no time.
But, in reality, most investors cannot take advantage of this edge.
Consider the coin flip experiment by Victor Haghani. You walk into a room with $25. There is a biased coin on the table, which gives a 60% probability for heads. If you make the correct call, you double your money; otherwise, you lose the bet amount.
You can bet any amount of your total portfolio on each bet, toss the coin as many times as you want, and change your bet amount each time.
Before going forward, we highly recommend you play this simulation and see how much you can make.
Haghani conducted the experiment on finance students from top colleges, analysts, and associates from leading asset management firms.
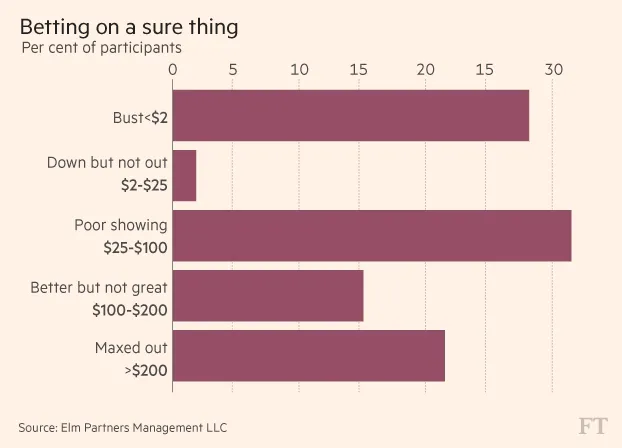
The results were disastrous. Even with a very apparent edge,
• 28% of the participants went bust
• 33% had less capital than they started off with
• Only 22% of participants had made >$200
The main problem you would face while playing this simulation is how much to bet.
Some of you might bet your total portfolio on one coin toss and bust out, while others might bet too little, which minimizes the total outcome but preserves your portfolio.
The right way to play this game would be to use the Kelly Criterion, which shows that you should only bet ~20% of your portfolio on every toss.
If you do this, you have a 95% chance of getting to the maximum payout of $250.
The researchers conclude by raising an important question:
If a high fraction of quantitatively sophisticated, financially trained individuals have so much difficulty in playing a simple game with a biased coin, what should we expect when it comes to the more complex and long-term task of investing one’s savings?
Kelly Criterion Bet Calculator: Optimizing Bet Sizes
Link :