@pitmaster reminded me about make_regression. It creates features for which you can control the number of informative (non-noise) features, correlation of the feature and the global amount of noise in the data.
I thought I would use it to answer questions like "How many noise factors can I add before ExtraTreesRegressor stops working?" I am not sure I can simulate stock data exactly but at least I know which are the noise factors and how may of them there are with make_regression as I can control that. That question was kind of interesting.
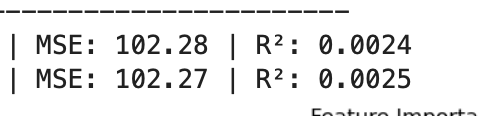
What was unexpected is that when I made more features informative the MSE increased (generally a bad thing)!!! While the R^2 increased (generally good). So contrary indicators with the MSE being suspect as it got worse when more features were informative.
MSE and R^2 for 2 models I was checking out with 10/50 informative features:

Now with 40/50 informative features:
So question:
-
Will MSE give you a false impression--at least when you are trying features? Honestly this is new and I am not sure how to interpret this. ChatGPT had some ideas but you can go to ChatGPT directly.
-
Is make_regression useful to us? And if so how.
I was comparing 2 models that Yuval and Pitmaster were recommending. Pretty much a tie (with these parameters) so maybe ignore that. If it was not a tie I probably would have modified the code to avoid getting sidetracked. I am just interested in the above questions.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# ----------------------------------------
# 1. Generate synthetic regression data
# ----------------------------------------
X, y, coef = make_regression(
n_samples=100_000, # scaled down for speed
n_features=50,
n_informative=40,
effective_rank=10, # adds correlation structure
noise=10.0,
coef=True,
random_state=0
)
# ----------------------------------------
# 2. Train/test split
# ----------------------------------------
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=1
)
# ----------------------------------------
# 3. Define Yuval's model
# ----------------------------------------
model_yuval = ExtraTreesRegressor(
n_estimators=100,
max_depth=8,
min_samples_split=2,
#min_samples_leaf=100,
max_features = 0.3,
random_state=42,
n_jobs=-1
)
# ----------------------------------------
# 4. Define Pitmaster's model
# ----------------------------------------
model_pitmaster = ExtraTreesRegressor(
n_estimators=100,
max_depth=None,
#min_samples_split=2,
min_samples_leaf=500,
max_features = 0.3,
random_state=42,
n_jobs=-1
)
# ----------------------------------------
# 5. Fit and evaluate Yuval's model
# ----------------------------------------
model_yuval.fit(X_train, y_train)
y_pred_yuval = model_yuval.predict(X_test)
mse_yuval = mean_squared_error(y_test, y_pred_yuval)
r2_yuval = r2_score(y_test, y_pred_yuval)
# ----------------------------------------
# 6. Fit and evaluate Pitmaster's model
# ----------------------------------------
model_pitmaster.fit(X_train, y_train)
y_pred_pitmaster = model_pitmaster.predict(X_test)
mse_pitmaster = mean_squared_error(y_test, y_pred_pitmaster)
r2_pitmaster = r2_score(y_test, y_pred_pitmaster)
# ----------------------------------------
# 7. Print comparison
# ----------------------------------------
print("Performance Comparison:")
print("-" * 40)
print(f"Yuval's Model | MSE: {mse_yuval:.2f} | R²: {r2_yuval:.4f}")
print(f"Pitmaster's Model | MSE: {mse_pitmaster:.2f} | R²: {r2_pitmaster:.4f}")
# ----------------------------------------
# 8. Optional: Plot feature importances
# ----------------------------------------
plt.figure(figsize=(12, 4))
plt.bar(range(50), model_pitmaster.feature_importances_, alpha=0.7, label='Pitmaster')
plt.bar(range(50), model_yuval.feature_importances_, alpha=0.7, label='Yuval')
plt.title("Feature Importances (Comparison)")
plt.xlabel("Feature Index")
plt.ylabel("Importance")
plt.legend()
plt.tight_layout()
plt.show()
# Show the true coefficients
print("True coefficients (non-zero features):")
for i, c in enumerate(coef):
if abs(c) > 1e-5:
print(f"Feature {i}: {c:.4f}")