@DesireX @test_user @WalterW @korr123 @yuvaltaylor and anyone interested,
TL;DR: This genetic algorithm approach seems to work well, and maybe P123 could automate something like this.
I modified my code to do something similar to what I perceive many are doing with optimizers—but with a genetic algorithm twist.
What’s the twist?
Genetic algorithms use crossover, which allows factors that perform well together to remain intact in the “genetic code” instead of being randomly split. This can help preserve synergies between factors that work well in combination.
The Results:
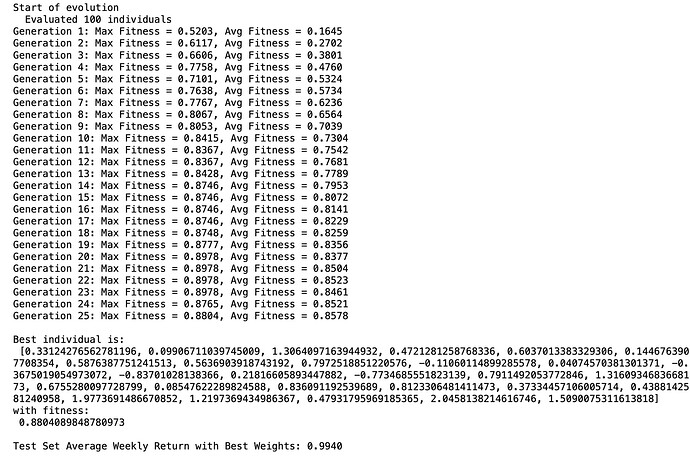
• The model was trained using a screening backtest.
• The test set which was out-of-sample achieved an average weekly return of nearly 1% (0.9940%) .
• The GA also produced optimized factor weights, making it possible to see which features were prioritized by the model. I did not include the names of the features.
Mathematically, this should converge to at least a local maximum with enough generations.
Here’s an example of the output, showing the progression across generations and the final results:
This raises an interesting question: Could something like this be automated within P123? Cross-validation could be added which I did not attempt with this code.
Code. You will need to create a column called 'ExcessReturn' that has your excess returns relative to the universe in a column.
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
import warnings
import random
from deap import creator, base, tools, algorithms
# Suppress warnings
warnings.filterwarnings("ignore", category=RuntimeWarning)
# ---------------------
# Data Loading & Prep
# ---------------------
# Read your eight CSV files and concatenate them
try:
df1 = pd.read_csv('~/Desktop/DataMiner/xs/DM1xs.csv', parse_dates=['Date'])
df2 = pd.read_csv('~/Desktop/DataMiner/xs/DM2xs.csv', parse_dates=['Date'])
df3 = pd.read_csv('~/Desktop/DataMiner/xs/DM3xs.csv', parse_dates=['Date'])
df4 = pd.read_csv('~/Desktop/DataMiner/xs/DM4xs.csv', parse_dates=['Date'])
df5 = pd.read_csv('~/Desktop/DataMiner/xs/DM5xs.csv', parse_dates=['Date'])
df6 = pd.read_csv('~/Desktop/DataMiner/xs/DM6xs.csv', parse_dates=['Date'])
df7 = pd.read_csv('~/Desktop/DataMiner/xs/DM7xs.csv', parse_dates=['Date'])
df8 = pd.read_csv('~/Desktop/DataMiner/xs/DM8xs.csv', parse_dates=['Date'])
df = pd.concat([df1, df2, df3, df4, df5, df6, df7, df8], ignore_index=True)
except FileNotFoundError as e:
print(f"Error: {e}")
raise
# Sort by Date and set as index
df = df.sort_values('Date')
df.set_index('Date', inplace=True)
# Replace NaN values in 'ExcessReturn' with 0
df['ExcessReturn'].fillna(0, inplace=True)
# Define features (using your provided list)
features = [Your features here]
# Check for missing features
missing_features = [f for f in features if f not in df.columns]
if missing_features:
print("Missing features:", missing_features)
features = [f for f in features if f in df.columns]
print("Using available features:", features)
# Split data into training and test sets
train_data = df[df.index < '2020-01-01']
test_data = df[df.index >= '2020-01-01']
X_train = train_data[features]
y_train = train_data['ExcessReturn']
X_test = test_data[features]
y_test = test_data['ExcessReturn']
# Standardize features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# Save the original indices for grouping by week later
train_dates = X_train.index
test_dates = X_test.index
# -------------------------
# Genetic Algorithm Setup
# -------------------------
# Define the fitness function: for an individual's weight vector, compute the dot product
# with each stock's features, group by week, select top 15 stocks, and take average return.
def evaluate(individual):
weights = np.array(individual) # Convert list to numpy array
# Compute predictions using a simple dot product
predictions = np.dot(X_train_scaled, weights)
df_scored = pd.DataFrame({
'date': train_dates,
'actual_return': y_train.values,
'predicted_score': predictions
})
weekly_returns = []
# Group by week using the date index
for date, group in df_scored.groupby(pd.Grouper(key='date', freq='W')):
if group.empty:
continue
# Select the top 15 stocks based on predicted score
top15 = group.nlargest(15, 'predicted_score')
weekly_return = top15['actual_return'].mean()
weekly_returns.append(weekly_return)
# If no weeks were processed, return a very low fitness
if not weekly_returns:
return (-9999.0,)
avg_weekly_return = np.mean(weekly_returns)
return (avg_weekly_return,)
# Use DEAP to define the individual and the genetic algorithm
creator.create("FitnessMax", base.Fitness, weights=(1.0,)) # We want to maximize average weekly return
creator.create("Individual", list, fitness=creator.FitnessMax)
toolbox = base.Toolbox()
# Attribute: a random weight for each feature; here we use a uniform distribution between -1 and 1.
toolbox.register("attr_float", random.uniform, -1.0, 1.0)
# Individual: a list of floats of length equal to number of features.
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_float, n=len(features))
# Population: list of individuals.
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
# Register evaluation, crossover, mutation, and selection operators.
toolbox.register("evaluate", evaluate)
# Crossover: blend crossover (adjust alpha as needed)
toolbox.register("mate", tools.cxBlend, alpha=0.5)
# Mutation: Gaussian mutation with mu=0 and sigma=0.2; indpb is the independent probability for each attribute to be mutated.
toolbox.register("mutate", tools.mutGaussian, mu=0, sigma=0.2, indpb=0.2)
# Selection: tournament selection with tournament size 3.
toolbox.register("select", tools.selTournament, tournsize=3)
# -----------------------
# Run the Genetic Algorithm
# -----------------------
random.seed(42) # For reproducibility
population = toolbox.population(n=100)
NGEN = 25
CXPB = 0.5 # Crossover probability
MUTPB = 0.3 # Mutation probability
print("Start of evolution")
# Evaluate the entire population
fitnesses = list(map(toolbox.evaluate, population))
for ind, fit in zip(population, fitnesses):
ind.fitness.values = fit
print(" Evaluated %i individuals" % len(population))
# Begin evolution
for gen in range(1, NGEN + 1):
# Select the next generation individuals
offspring = toolbox.select(population, len(population))
# Clone the selected individuals
offspring = list(map(toolbox.clone, offspring))
# Apply crossover and mutation on the offspring
for child1, child2 in zip(offspring[::2], offspring[1::2]):
if random.random() < CXPB:
toolbox.mate(child1, child2)
del child1.fitness.values
del child2.fitness.values
for mutant in offspring:
if random.random() < MUTPB:
toolbox.mutate(mutant)
del mutant.fitness.values
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
# Replace the old population with the offspring
population[:] = offspring
# Gather all the fitnesses in one list and print stats
fits = [ind.fitness.values[0] for ind in population]
print(f"Generation {gen}: Max Fitness = {max(fits):.4f}, Avg Fitness = {np.mean(fits):.4f}")
# Identify the best individual in the population
best_ind = tools.selBest(population, 1)[0]
print("\nBest individual is:\n", best_ind)
print("with fitness:\n", best_ind.fitness.values[0])
# --------------------------------
# Evaluate on the Test Set
# --------------------------------
def evaluate_on_test(individual):
weights = np.array(individual)
predictions = np.dot(X_test_scaled, weights)
df_scored = pd.DataFrame({
'date': test_dates,
'actual_return': y_test.values,
'predicted_score': predictions
})
weekly_returns = []
for date, group in df_scored.groupby(pd.Grouper(key='date', freq='W')):
if group.empty:
continue
top15 = group.nlargest(15, 'predicted_score')
weekly_return = top15['actual_return'].mean()
weekly_returns.append(weekly_return)
if not weekly_returns:
return -9999.0
return np.mean(weekly_returns)
test_performance = evaluate_on_test(best_ind)
print(f"\nTest Set Average Weekly Return with Best Weights: {test_performance:.4f}")
Suggests optimal features based on data patterns
