LightGBM and interactions

[Jrinne]

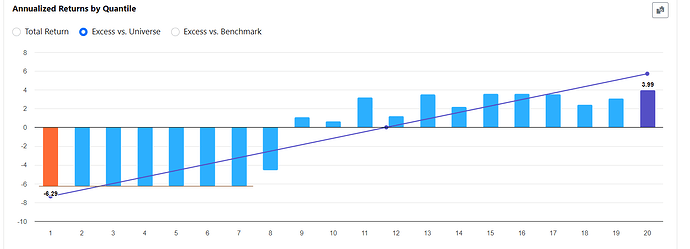
Tree models, including LightGBM, inherently include interaction of features. If you find tree models modestly outperforming linear models one reason may be that LightGBM is able to capture interactions in its model.

I think that if you find this improvement modest it is because it allows all interactions including noise interactions.

This negative aspect can be controlled to some extent in LightGBM with interaction constraints. From LighGBM's documents:

• interaction_constraints ︎, default = "", type = string
  • controls which features can appear in the same branch
  • by default interaction constraints are disabled, to enable them you can specify
    • for CLI, lists separated by commas, e.g. [0,1,2],[2,3]
    • for Python-package, list of lists, e.g. [[0, 1, 2], [2, 3]]
    • for R-package, list of character or numeric vectors, e.g. list(c("var1", "var2", "var3"), c("var3", "var4")) or list(c(1L, 2L, 3L), c(3L, 4L)). Numeric vectors should use 1-based indexing, where 1L is the first feature, 2L is the second feature, etc
  • any two features can only appear in the same branch only if there exists a constraint containing both features

[ZGWZ]

@Jrinne

If you find tree models modestly outperforming linear models may be one reason.

This is the main, if not the only, reason. Attempts to isolate the sources of nonlinear model performance often find that the difference is only in the interaction term part.

However, the inclusion of interaction terms in linear models is often not considered a valid approach in papers, even though it is a nice way to distill/interpret nonlinear models.

[Jrinne]

@ZGWZ

This is the main, if not the only, reason. Attempts to isolate the sources of nonlinear model performance often find that the difference is only in the interaction term part.

However, the inclusion of interaction terms in linear models is often not considered a valid approach in papers, even though it is a nice way to distill/interpret nonlinear models.

Thank you for your input ZGWZ. In addition to supporting the idea that interaction variables can be important you have cautioned against using interaction variables in linear models. This is important, to me anyway, and I wish to research it further. I have included this interaction for others who may be interested in researching this topic.

I asked Claude 3 this question after it gave me a more general answer about interaction variables: "Make it specific to adding interaction variables in linear models. Make sure to include pros AND cons without bias." For Claude 3 one has to copy the title and author and google that. With about a 60% success rate on finding the exact article. I have not started on these articles yet.

A: "Certainly. I'll provide a more focused list of papers that specifically address adding interaction variables in linear models, ensuring a balanced view of both pros and cons. Here's a revised list:

1. "Interaction Effects in Econometrics" by Balli and Sørensen (2013)

   • Pros: Discusses how interaction terms can capture important nonlinear relationships.
   • Cons: Warns about potential multicollinearity issues when including interactions.

2. "To Include or Not to Include: The Impact of Interaction Effects in Regression Models" by Brambor et al. (2006)

   • Pros: Argues for the importance of interaction terms in certain contexts.
   • Cons: Highlights potential issues with interpretation and significance testing.

3. "Regression with Interaction Effects" by Jaccard and Turrisi (2003)

   • Pros: Provides comprehensive guidelines for using interactions in linear models.
   • Cons: Discusses challenges in interpreting complex interaction effects.

4. "Interaction Terms in Poisson and Log Linear Models" by Karaca‐Mandic et al. (2012)

   • Pros: Demonstrates how interactions can improve model fit and predictive power.
   • Cons: Cautions about the difficulty in interpreting interaction effects, especially in non-linear contexts.

5. "The Importance of Properly Measuring and Modeling Interaction Effects in Strategy and Management Research" by Andersson et al. (2014)

   • Pros: Emphasizes the theoretical importance of interactions in certain fields.
   • Cons: Highlights common pitfalls and misinterpretations when using interaction terms.

6. "Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences" by Cohen et al. (2003)

   • Pros: Provides a comprehensive guide on when and how to use interaction terms.
   • Cons: Discusses the complexities and potential pitfalls of including multiple interaction terms.

7. "Interaction Effects in Multiple Regression" by Jaccard et al. (1990)

   • Pros: Offers practical guidelines for incorporating and interpreting interaction effects.
   • Cons: Addresses issues of multicollinearity and reduced statistical power when including interactions.

8. "Regression Discontinuity Designs in Economics" by Lee and Lemieux (2010)

   • Pros: Discusses how interaction terms can be crucial in certain econometric models.
   • Cons: Highlights the sensitivity of results to model specification when including interactions.

Key points to consider when presenting these to P123 users:

1. Interaction terms can capture complex, non-linear relationships that simple linear terms might miss.
2. Including interactions can lead to multicollinearity and interpretation challenges.
3. The choice of which interactions to include should be guided by theory and domain knowledge.
4. Proper interpretation of interaction effects requires careful consideration of the entire model.
5. While interactions can improve model fit, they may also increase the risk of overfitting.
6. The statistical significance of interaction terms should be interpreted cautiously.

This balanced list provides a comprehensive view of both the benefits and challenges of including interaction terms in linear models. It should help P123 users make informed decisions about whether and how to incorporate interaction terms in their own models."

I note ridge regression can handle some collinearity issues.

Jim

[pitmaster]

Any example of how interactions (a * b) should be computed ?

What about forcing a and b to be non-negative:
Max((SalesTTM / EV ), 0) * Max(Surprise%Q1, 0)
This would works like ReLu activation function.

[Jrinne]

Hi Piotr,

Nice! For those not familiar and following, ReLU (Rectified Linear Unit) is often the default activation function for neural-nets. But obviously it can be used elsewhere as Piort suggest here.

Clearly it would be a good contender for two features that are monotonically increasing. Using the product and ranking the product would ensure that both features are highly positive if one is selecting 15 - 30 of the highest ranked stocks in a port.

Less sure about the general case where one or both features might have a different distribution. While I have been aware of interaction terms for a long time, I am pretty new to actually using it for investing models. So just not sure and don't really know.

So far I have mostly been wondering how to use what little "domain knowledge" I have for selecting interaction variables.

I have long thought that at P123 we are selecting companies with extreme valuation ratios (like price to earnings) that are about to revert-toward-the-mean. That this is the short answer to why our ports and ranking systems work.

But obviously it is preferable if we buy companies that will revert-toward-the-mean by increasing price and not reducing earnings going forward.

(Value ratio) * (growth), or (value ratio) * (earnings estimate revisions) could explicitly select companies with value ratios that are about to improve by increasing the price.

BTW, to your suggestion, these features (value ratios, growth and earnings estimate revisions) would generally be monotonically increasing factors and your ideas on the ReLU-like activation function might well be an improvement over a simple product of features, I think.

Claude 3 suggested something that is a direct answer to:

@pitmaster

Any example of how interactions (a * b) should be computed ?

Specifically Claude 3 thought normalization of the features might be useful;"

"Normalization:
When working with interactions, especially across different types of ratios or indicators, normalizing the components before interaction can be helpful. This prevents one factor from dominating due to scale differences."

This could be done easily with P123's z-score function. Z-score can be used in multiple places with P123. Ranks might be fine for normalization too but not sure if raw values will work as well

Jim

[ZGWZ]

Considering the two factors are good, this is not a promising result.

Many papers talk about what interactions are useful, you can check them or just search yours from the downloaded data.

[yuvaltaylor]

A composite rank node is an excellent way to get an interaction of factors.

Keep in mind that many factors are themselves interactions. For example, recent sales acceleration, which is in the P123 Core Growth ranking system, is %(SalesGr%PYQ, SalesGr%TTM). So that's the interaction of PYQ and TTM sales growth, with the latter having a negative effect and the former a positive one.

Beneish's M-Score is the interaction of eight different factors using a linear regression.

[Jrinne]

Hi Yuval,

Do you think, more generally, that optimization with the P123 classic optimizer can allow for interactions?

Question to Claude 3: Suppose I had a ranking system that ranked stocks by weights of factors. And unlike say, a ridge regression I just optimized for the 15 best performing stocks rebalanced weekly. Would this method—unlike standard linear regression— be including interactions..

Claude 3 answer: "Yes, this method would implicitly include interactions, unlike standard linear regression.

By selecting only the top 15 stocks based on a weighted ranking of factors, your approach captures complex, nonlinear relationships between the factors that aren't explicitly modeled in standard linear regression. These relationships effectively act as interactions.

The weekly rebalancing and focus on top performers allows the model to adapt to changing factor interactions over time, potentially capturing synergies between factors that become important only under certain market conditions or when other factors align in specific ways.

However, unlike explicitly modeled interactions in regression, these interactions in your ranking system are implicit and not easily quantifiable or interpretable. They emerge from the nonlinear selection process rather than being deliberately specified in the model."

ChatGPT: "Yes, if your ranking system optimizes for the 15 best-performing stocks based on a combination of factor weights without imposing a linear structure like standard or ridge regression, it could implicitly capture interactions among the factors…...Thus, your method is indirectly modeling factor interactions, as the ranking and selection process naturally favors stocks where combinations of factors perform well. "

I think that too (which is why I asked the LLMs in the first place). I would be interested in what others think.

Jim

[feldy]

I use a couple interaction terms in some of my ranking systems using FRank(A)*FRank(B) to magnify the effect when both factors are high (or both are low). There's a little more color in this thread, and in one of Marco's replies, he highlights why this approach is different from a weighted average inside of a Composite:

@marco

The use-case is interesting. For example if two factors rank 60/60 then they average 60; the same as if one ranked 100 and the other 20. Doing a product does favor 60/60 quite a bit more than 100/20.

Jim, I'll have to give your theory on whether a top 15 optimization would capture this if it was based on a weighted ranking of factors. My intuition says no as that relationship couldn't be represented in the linear formula of individual terms but I have to give it more thought.

[Jrinne]

Feldy,

Thank you for sharing your insights on how to normalize this with frank(). Your link shows the potential problems with z-score as you know.

Jim

[yuvaltaylor]

Testing and optimizing ranking systems take factor interactions into account quite heavily, as do multiple regression models. One of the problems with testing individual factors alone and creating ranking systems based on those is that they do not allow for factor interaction.

I use some factors that test terribly on their own. The reason I use them is that they interact with other factors quite well. Examples include accruals and low/negative profit margin (which can be predictive of earnings growth).

[ZGWZ]

You're not talking about interactions, but complementary effects between factors.

[Jrinne]

I get your point and I think you are probably right with regard to using the P123 optimizer (without conditional variables and/or products of variables). Probably should not be called interactions.

Thanks.