All,
If you happen to want a prediction of the returns you can get it from P123 classic (if you assume linearity).
You can convert ranks into predictions (and vice versa) using a linear regression model, if you assume linearity. This means you are assuming a linear relationship between the ranks and the value of the returns
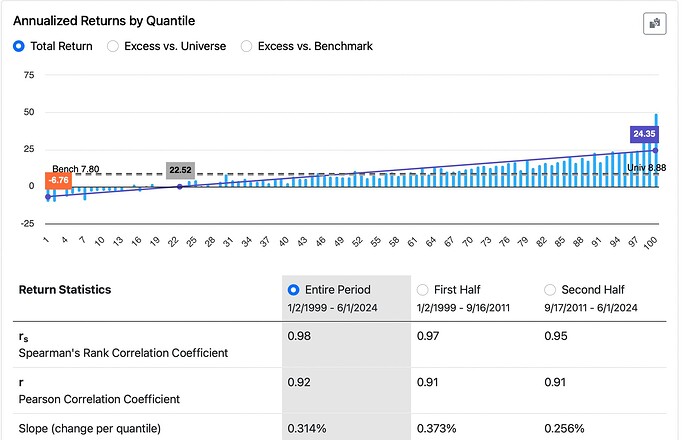
For this ranking system (with 100 buckets), you can calculate predicted returns using the formula:
{Prediction} = 100 * {slope} *{rank} + {intercept}. Note that the returns are annualized here.
In this case the slope is given to you by P123: 0.314. The intercept is just the return of to lowest bucket: -6.76.
For linear models, ranks can be derived from predictions and vice versa. Essentially, if you have a linear relationship, converting between ranks and predictions involves simple linear transformations. For non-linear models you can sort the predicted returns to get a rank but the transformation is not as straightforward as it is with linear models.
BTW. Does this rank performance look linear to you? Maybe if you call the last few buckets outliers (especially the last bucket). The stocks you are buying in other words. But if you use the term "slope" that implies an assumption of linearity (as does Pearson's Correlation).
Jim