What do folks consider the success threshold for a investment system?

General
1

I have started investigating ML as a method of building an investment system. It has got me thinking about how to determine what is worth putting my money into. Be that savings accounts, ETFS, multi-factor ranking systems at P123, or ML using ranks from P123.

Below is my thought process at the moment. I am interested in what other folks think as well!

All annual numbers I mention should be an average over about 10 years if the method is subject to significant volatility. I would also personally say it would be difficult for me to sit through more than a year or so of a 50%+ drawdown so that is probably my limit on the potential downside of a method in a back test.

  1. Start with the easiest/safest investments: must beat 5% annual returns
  • Fidelity currently returns almost 5% on cash in an investment account. So if my method returns less than that annually I would rather hold cash right now.
  • VTI is a very diversified ETF and is around 6% annual since it was released (less dividends). I also need to do better than this
  • Private REITs can return 5-10% dividends as well and are easy to invest in
  1. Start considering more volatile investments, but still low effort: must beat 10% annual
  • Easy ETFs like VOO and QQQ are good starters and at least in the last 10 years have done very well
  • Stock picking has been a mixed bag for me and I am very guilting of just buying what sounded great (over about 5 years my accounts range from 20% annual to -50% (thanks crypto), but average about 9% annual)
  1. Multi factor ranking systems: not really sure what I should consider a baseline here, maybe 20% annual?
  • I should probably consider a multi factor ranking system about the same as holding an ETF as many ETFs are just screens anyway…
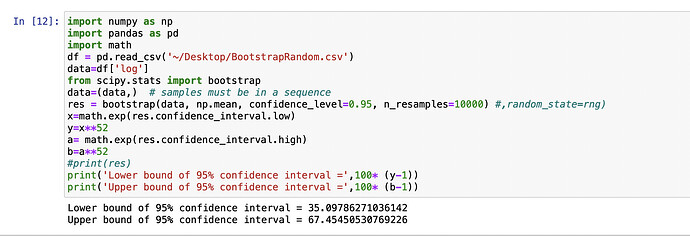
  • Back testing robustly is hard. I can squeeze a lot out of a back test even with something like core combinations on the Prussel 2000 universe (20% annualized or more) and I am inclined to believe most of that is due to overfitting as I used a fairly intelligent algorithm to explore the best weights for 2012-2018 out of the 10 year back test. So its a bit difficult to say when I have found something that I can feel confident putting a lot of money in compared to less effort options like VOO with OOS returns.
  • That being said the upper bounds for what multi factor ranking systems and smart buy and sell rules can get you are pretty high. At least over 30% per year, and if the weekly email I get is to be believed maybe even over 100% is achievable some years.
  1. My last category is ML and is exploratory at the moment and entirely relative: metric for success, must be better than an optimized linear multi factor ranking system
  • In other words the returns of the ML model out of sample (OOS) must be better than a robustly optimized ranking system, also OOS, using the same or similar factors and signals.
  • This is mostly because multi factor ranking systems are simpler to maintain and understand. This may change when P123 rolls out their AI system, but for now if I do ML I am 100% responsible for making sure my code is working properly and updating it as needed.
2

My advice is to start investing in multifactor ranking systems relatively soon. There are two major things to focus on: creating a good ranking system and a consistently good portfolio management strategy. Neither has to be perfect. By starting to put your money in them, not only will you benefit from compounding, but–and this is very important–you’ll benefit from your experience. My investing experience using algorithmic systems has taught me much more than any amount of backtesting ever could. Mistakes will teach you extremely valuable lessons, but only if real money is behind them. They’ll make you look carefully at why exactly you’re buying such-and-such a stock. Without putting actual money behind your efforts, they’ll all be for naught. It’ll be like developing a chess strategy without actually playing any chess.

3

I don’t think anyone at P123 would disagree with this. The ranking system and ports make it EXTREMELY convenient.

And some methods/algorithms can be fit back into a ranking system and backtested or even cross-validated within P123.

I have been posting a lot about random forests and XGBoost recently because you have stimulated my interests.

But my present ML system determines my rank weights and I rebalance a port now, just like everyone else. My method is fully ML by any definition. I originally trained it until about 2015 then did a holdout test sample that did well.

So really the only thing that makes it special is the holdout test sample. Others are doing things that are similar to what I have done. Using mod() for example which I have always thought was a good idea.

I could have (probably should have) done train, validate, holdout sample and done recursive feature elimination using cross validation. But I did not, to put it simply. It was too hard at the time or I was just lazy.

I then retrained on all of the data available. I might retrain it once per year but it is extremely stable. My live port results are not statistically significant by any means but I am pleased.

THE ONLY THING I CONSIDER SPECIAL ABOUT MY ALGORITHM is that I had a holdout test sample.

Otherwise, Yuval, Whycliffes, Walter etc have great ‘algorithms’ whether you want to call them ML or just ‘smart things to do.’

Anyway, I think many would agree that you can steal some ideas from ML and still use ranks. I do.

TL;DR: I like this stuff but it does not have to be hard.

Jim

4

For sure agree that putting real money down is needed to really start the learning process. And I have done so with one of the Portfolio123 models as a starting point. So far I have mostly learned there are a lot of pump and dump stocks out there. Not sure how to code avoiding them into P123, but that is off topic.

I think my real question is how do I go from “play” money level of confidence to enough invested I can live on the returns. I am not talking about growing my portfolio, but allocating my existing assets towards the strategy. For example I currently hold say 75% ETFs in my IRA account and 20% to a multi-factor ranking system. I think if I was more confident I would flip that ratio.

5

Jonpaul,

I use Bayesian model averaging—which is not unlike the Bayesian optimization you use in your ML model. Basically, I make my model prove itself out-of-sample (funded results). Allocating more funds to it after (hopefully) it has proven itself. I would allocate less if it were not proving itself out-of-sample.

I looked at the “hedge algorithm” for expert advice but it is kind of clunky: Prediction with Expert Advice. But it can be updated in a spreadsheet (adjusting the weights according to how your strategies are doing). It does offer some performance guarantees relative to the performance of the optimal strategy (in hindsight) but they are not very strong guarantees. I like Bayesian model averaging. And it turns out to be easy for me to do.

Here is a resource that I can recommend for those having trouble sleeping at night: Prediction, Learning, and Games

You can get many “Expert Advice Algorithms” with enough detail to apply them from this text. But I like what Walter says below. It does not have to be numerically exact.

Jim

6

I think my real question is how do I go from “play” money level of confidence to enough invested I can live on the returns.

Time.

This may not be common, but for many of my models, I let them simmer for a year. The out-of-sample performance should provide some basis for allocating funds.

When that history is not available, I start with small allocations and apply strict risk management. That may not be ideal, but some models are too good to leave on the shelf.

2 Likes
7

There are a number of different ways of approaching this: it’s the classic question of balancing risk and returns. I’ll go over a few approaches, but I just want to get a few things out of the way first, which you probably already know. #1. Never risk money that you need for basic living expenses. That should always be in a risk-free asset. Maybe only 3 or 6 months’ worth, maybe a year or two’s, maybe five years’ worth. #2. In my opinion, ETFs have only three true advantages over a well-diversified selection of 30 or so well-chosen stocks. First, there’s a major tax advantage, which doesn’t apply to IRAs. Second, you’re not paying transaction costs. Third, you don’t have to sweat: you just park your money in them and leave them alone.

As for allocating your assets to various strategies, my approach is to invest in the strategies that you think will bring you the highest returns, risk be damned. But if you’re withdrawing a substantial sum every year, then risk must be taken into consideration. For doing that, most people look to the Sharpe ratio, but in my opinion that’s really badly flawed. Much better, in my opinion, is the Omega ratio. Ask ChatGPT about the difference. To calculate the Omega ratio, you set a threshold of acceptable returns. You then take the monthly return of your portfolio and subtract that threshold. Then you add up all the positive results and the absolute value of all the negative results, and divide the first by the second. Do that with various portfolio options and go with the one that gives you the highest omega ratio.

For example, I was trying to decide how much of my portfolio to devote to put options given that my out-of-sample returns on those have been significantly higher than the return on my stock positions and that they have a negative correlation (though only slightly: -0.06). Obviously, I’m not just going to sell all my stocks and buy puts instead. So I set a threshold of 0.8% per month (10% annually) and used Excel to maximize the omega ratio given x% of my portfolio to stocks and (1-x)% to puts. The result was a recommendation to invest 25% to 30% of my portfolio in put options. If I’d used the Sharpe ratio, it would have recommended a higher percentage. I’m not about to put that much of my portfolio into put options, but it was nice to know I could safely go higher than 6%, which had been my threshold.

Another option is to use a modified Sharpe ratio, whose formula is (geometric mean of portfolio return - geometric mean of risk-free return) / (standard deviation^2 - skew * standard deviation^3 + 0.25*(kurtosis - 3)*standard deviation^4)^0.5.

I have relied a great deal in the past on Monte Carlo simulations. That might be very helpful if you’re really uncertain about potential returns on your various approaches. I did a lot of Monte Carlo simulations before I decided to take out a large cash-out mortgage and put it into stocks; I did a lot of them before I decided to devote a certain percentage of my returns to a charitable foundation. They give you a good sense of worst-case scenarios given various approaches and various stock-market returns.

Lastly, you might want to consider a hedging strategy for risk reduction. As I’ve said, I like to buy put options on stocks that rank highly on reversed ranking systems that I’ve designed for this purpose, but put options on these kinds of stocks can be extremely overpriced, and it’s important not to overpay for them. I don’t recommend shorting, but I really do like the approach of these authors if you don’t want to spend the time and energy studying option pricing: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4378071

1 Like
8

I just want to add to this in a positive way. Not for this exact use, but I use a lot of bootstrapped confidence intervals for different things. I’m not sure there is a big difference in the answers they give. I would not disagree with someone saying they liked one or the other for some reason.

Monte Carlo simulations can be done in a spreadsheet. Bootstrapping might need Python.

10

I’ll have to look up how to do both methods. I think with python and help from chatgpt both should be easy enough to implement.

I assume both methods are to give approximate bounds on performance in the future based on past volatility?

11

Jonpaul,

Editied Aside: I do think this is on-topic for the thread as one would want to know the range of possible results or confident interval for a model before deciding to invest in it. This is one way to begin to get that. For a sim with in-sample results one would also have to consider overfitting, regression-to-the-mean etc but it is a start. For out-of-sample results one should be concerned about the multiple-comparison problem. You can get an exact number for this however if you count the number of models you are looking at (like with the designer models where you know the number of models). Maybe use the Bonferroni correction which considers the number of models you are looking at.

Yes. Monte Carlo simulations are used a lot for financial planning. Telling older couples their chance of their investments going to zero if they live to 100. I did not read the details but something like Yuval was doing I believe.

Bootstrapping will do the same thing.

Both are used in statistics too. Bootstrapping has the advantage of being non-parametric which is nice for stock data. I.e., no assumption that the returns are normally distributed (which they are not).

As an example, downloaded the weekly returns for a sim from P123. In the spreadsheet I created a column called ‘log’ for log returns. i.e., ln(1+[B2]/100). [B2] is the cell in the spreadsheet for the 'Model" column.

Here is an image of the 95% confidence interval for the returns of the sim. Note, you can take the meaning of the 95% confidence interval as being the same as you would with a t-test but this is non-parametric:

Screenshot 2023-08-28 at 4.14.21 AM
Screenshot 2023-08-28 at 4.14.21 AM1984×684 194 KB

For out-of-sample data this could have real meaning regarding whether your model has a statistically significant edge.

One could consider using this for the designer models. I do not think it would be too weird for a site that does machine learning and is trying to attract the Kaggle crowd (total geeks meant in a good way).

And again, more and more we just need the downloads (for the designer models’ returns for example to bootstrap those results). Specific feature request are becoming less-crucial to members interested in specific or advanced methods or metrics.

Maybe I would want to run a Bayesian t-test. I have no doubt that all of the programmers at P123 would be involved in something more important that making Bayesian t-tests results available for the designer models. But the download might allow for many features at once with less coding.

ChatGPT could code this. I think I coded this before ChatGPT but I am losing track what part of saved code I wrote. :slight_smile:

Jim

12

I wondered how conditional value at risk (CVaR) was calculated and if bootstrapping could be used to calculate the conditional value at risk. Turns out that both Monte Carlo Simulations and bootstrapping are used according to ChatGPT. I am not sure which is more common. But sometimes they use both to calculate CVaR:

“In practice, banks and other financial institutions often use both methods (as well as others, like the variance-covariance method) to compute the CVaR and compare the results. This provides a more robust estimate of the risk and accounts for different sources of uncertainty.”

Thank you Yuval for introducing this topic to the forum. Turns out Monte Carlo simulations can be used in a lot of places.

ChatGPT was simplifying a little for me, perhaps, but CVaR can be calculated as a rolling Monte Carlo simulation or a rolling boostrap—taking the mean or median of the lower interval. Again, pretty much what Yuval outlined.

Jim