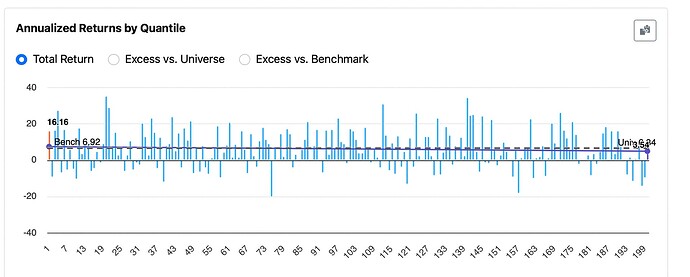
So I decided to take a look at one of my ports using the literal meaning of p-value which is: "The probability of obtaining results at least as extreme as those observed,…" Including something about a null hypothesis in the full definition.
Using random() for my ranking system set to the same period as my port gave me the result of 200 screens selecting about 18 stocks (close to 15). Each bucket is like an 18-stock screen or a sim with no transaction fees.
By chance alone seven 18-stock screens (or the equivalent) did as well or better. p-value = 7/200 = 0.35 (by definition).
Or p = 0.035 with no BS. No normality assumption; no worry about skew. No proofs or assumptions--other than "true by the definition of p"—needed.
Let someone else worry about whether the data is normally distributed, whether it should be a paired or unpaired t-test using raw or excess returns. And you could worry even more if you wanted to. Excess returns relative to my universe or my benchmark? Maybe I should use bootrapped confidence intervals because it is non-parametric method? Hmmm… a Bayesian t-test would be nice. uhhhh with a normal distribution, t-distribution prior or a cauchy prior? Is a normal prior conjugate and why do I care?…..
Let them worry and call BS on them (or me) if you have done the above method and get something different.
If you did this several times and averaged the results, it is probably the most accurate way to do this with the least number of assumptions (i.e., you only assume that you got the definition of p-value, with your null hypothesis, right for your specific problem).
Checked for accuracy with Claude 3 Sonnet with this response: "Your method is a straightforward, empirical application of the p-value concept. It avoids many assumptions required in parametric statistical tests, making it particularly suitable for financial data which often doesn't follow normal distributions." Oh, and the obligatory: "However, it's important to note that past performance doesn't guarantee future results." ![]()