More deterministic: pr52w%chgind + Frank("Mod(stockid,3)")/100—or better yet, Frank("pr52w%chgind") + Frank("Mod(stockid,3)")/100 to ensure the offset remains small relative to the main feature’s rank.
You’d likely need to apply a similar technique to every feature in your ranking system—especially those prone to frequent ties.
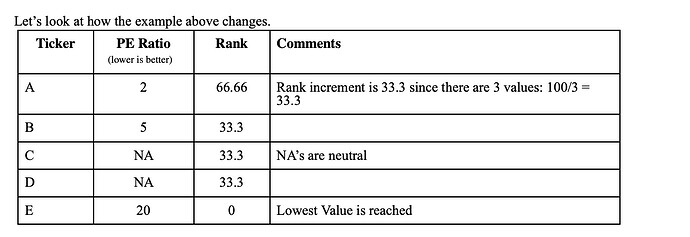
This adds a small, reproducible offset based on StockID to break ties consistently.
It directly addresses the original issue of pr52w%chgind not being reproducible across runs. A similar approach can also support reproducible dithering—though Random() would offer much finer variability if reproducibility weren’t a requirement.
The main limitation of Mod() is that it typically generates only 10 distinct values. More elaborate constructions—such as averaging multiple Mod() expressions—can expand that range, but quickly become unwieldy and is still quite limited. Random() would provide far better resolution, but is currently not reproducible in P123.
@marco: Increasing the precision of the ranking system—e.g., by allowing more decimal places—would let us use something like Frank("Mod(stockid,3)")/1000 instead of dividing by 100. This would ensure that the added offset is small enough not to alter the underlying rank order.
If it’s not too computationally expensive, I think users will increasingly adopt this approach, and higher precision would make it functionally perfect.
And in fact, rounding behavior—with the current level of precision—may account for a small number of the apparent ties we’re seeing.
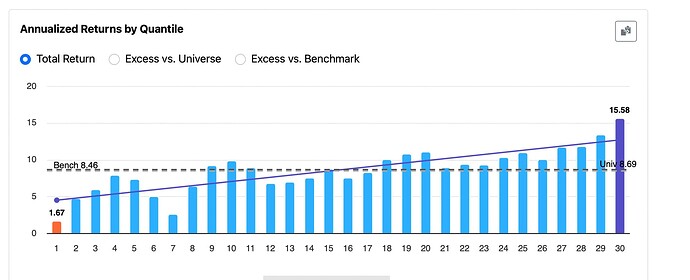
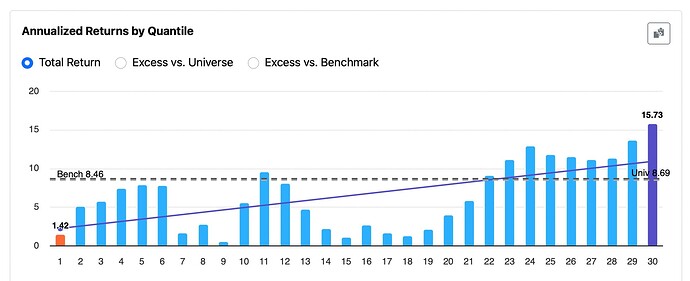
P123 team: Even if this isn’t widely adopted by others, I’d personally like to use dithering to improve the smoothness of rank performance tests and reduce the bias from ranks or buckets that show zero (or artificially low) returns—especially in the middle ranks.
There’s really no informed debate that assigning NAs a single, undithered value is the root cause of the chronic distortion observed in the middle rank buckets of performance tests—when a significant number of NAs are present. There’s also a workable solution—one that could be made functionally perfect with increased precision. I believe the improvement would be noticeable from a marketing standpoint—for both retail and enterprise investors.
Higher precision would give me confidence that I’m not inadvertently altering the true rank order. I’d really appreciate it if you could evaluate whether increasing precision is a significant programming challenge, and whether it would meaningfully impact computational resources.
To be clear, I wouldn’t need any additional changes—just higher precision. I don’t require dithering to be deterministic myself, though that may matter more for other users and other use cases.
The actual dithering I can do myself with the above code: I just need better rank precision.