Evaluating R2G out of sample performance

Models
21

Tom,

If a perfect formula for predicting out of sample returns would exist, then I’d be typing this post from a lounge chair in the Bahamas… so any formula will have flaws. And the conclusion for this particular one in a couple of years might just be that it worked great… in 2013 only.

I had thought about the number of holdings as well. This cannot work for large numbers of holdings, because at some point you’ll just be getting market returns and an alpha of 0 by definition. But the majority of R2G models have between 5 and 20 holdings, so that’s ok. (In fact, there are some with more holdings, and then the “predicted” return is overstated!). Statistically speaking, number of holdings was only barely significant, as I mentioned before. This means that it may be a false positive and may not have any predictive value. But theoretically it does make sense to me.

Similar for turnover I guess. Most models will have turnover in reasonable ranges. Higher turnover means more trades, and less chance of random results in backtesting. Oliver has mentioned several times that a large number of trades (either many holdings, or high turnover) is important for out of sample robustness. I haven’t tested that exactly, but my results do point in that direction.

Btw, there is a mistake in the previous post. I didn’t divide by turnover, but I multiplied by “Turnover/100 / 365” (so it’s a daily turnover percentage). Just the label in the scatter plot and the header of the data column in the CSV are wrong. I also multiplied with turnover in the first post. I actually divided by 1/Turnover, hence my confusion.

22

pvdb - I’ve been reading your post(s) over and over and I cannot clearly understand everything that you wrote. (It is probably me.) You didn’t provide the formula you used to calculate the compounded version of GSD and the file you provided is a CSV file so I couldn’t extract any formulas from a spreadsheet. Also, it isn’t clear to me if you published any graphs with the compounded version - perhaps you did but I don’t understand all the various graph axis. Also, I don’t understand what “annualized excess predicter” is (graph with best results).

I am going to say again that I believe the correct way to do this is with the compounded version of GSD. There is an interaction going on between GSD and turnover that is probably making the simple GSD look good. The effect that turnover has on results won’t truly become clear until the graph is computed with the compounded version.

Anyways, I do appreciate the work you have done and am sorry for being a pain. Its just that I have to give my feedback.

Tom - I had a look at your presentation but I don’t feel there is enough there for a proper peer review. The first thing that needs to be established is how the criteria for system selection was arrived at, for both cases. This is to ensure that there is minimum bias in the study. Second, you need to make sure that the same timeframe is used in all cases. (Same applies to pvdb). I know it is easier to process results given by P123 “since launch” or “since inception” but this often leads to unforeseen biases. For example, many largecap systems were not launched at the start of R2G. Some came along later and were not as exposed to the unlimited QE mentality that persisted for the first few months of R2G’s existance. There is also the experience factor. Regardless of how long providers have been with P123, most only have experience with micro/smallcap models. They have been driven to start producing higher liquidity models once R2G started. This is a good thing, not a bad thing. Even if results are no better than the baseline market (for now), model providers will learn or sink. In the long run this will benefit subscribers as there is no benefit to having too many smallcap systems out there. In my opinion, R2G is the best thing that has happened to P123, because it allows all of us to look and learn based on real systems with real money being put into them. The alternative is the “winners circle” which in my opinion is smoke and mirrors.

Steve

23

Steve,

No worries, I appreciate your feedback. I’m not sure what you don’t understand exactly, so just ask if this post doesn’t answer all your questions.

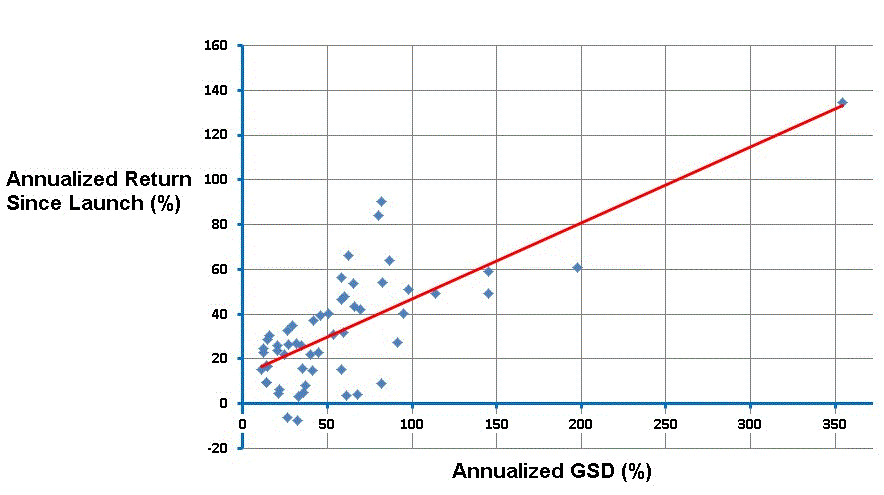
The scatter plots show the relation between annualized excess return since Launch (labeled Ann Excess Launch on all charts) versus another variable of interest. Each point on a scatter plot is one R2G model. Let’s take the outlier that is clearly visible on all charts in the upper right corner. This model has Ann Excess Launch of close to 120 percentage points. On the Y axis you can see how this model scores on a given variable, for example it had a GSD of around 0.45 (% per day) and an Annualized GSD of over 400 (% per year). The histograms to the left and on the bottom show how many models fall into a certain range of values, but that’s not important here.

The red lines in the scatter plots show the best linear relationship (trend line / regression line). You can easily create these plots in Excel yourself. Just select two columns, insert a scatter plot (XY chart), and add a linear trend line. Please note that the red lines in the scatter plots have different slopes and intercepts. The slope of the red line is also not necessarily exactly 1. It’s simply the best linear approximation of the relationship between the two variables.

Now, the reason for doing this is to see whether there is a systematic and relevant relationship at all. If there is no meaningful relationship at all, then the points in the scatter plot would all over the chart and you wouldn’t see a pattern at all. You can try to make a scatter plot of some variables I listed under “No longer significant according to a t-test” against Ann Excess Launch to see what I mean. (Nevermind the word t-test or R2 value.)

If there would be a perfect linear relationship, then all the blue circles in the scatter plot would be exactly on the red line. The more dispersed the blue circles are, the less clear the relationship is (up to non-existent if the points are scattered all over the chart). So the red line helps to see how strong the relationship is, by judging the distance from the blue circles to the red line.

So in essence I charted all variables I listed against Ann Excess Launch and judged the ‘fit’. Well, I didn’t actually do that manually, but I ran a script that computed the R-squared and t-test for each combination, and those values can be used to interpret the fit. Higher values of R2 mean that there is less dispersion around the red line, whatever that red line would be for that particular combination of variables.

In fact, you can do this for any number of variables against Ann Excess Launch. See http://en.wikipedia.org/wiki/Linear_regression. I tried it for combinations of up to two variables against Ann Excess Launch. The R2 is highest when you use AvgReturn*Turnover and LOG(Holdings) as the two variables. This means that those two variables are best for explaining the Ann Excess Launch based on the data we have about R2G models in this particular period, and, if the relationship will persist in the future, then it’s also the best prediction of future performance. This is a big if. (And besides, linear regression makes a number of assumptions which may or may not hold).

The exact formula I used to calculate Annualized GSD is (((1.0 + GSD / 100.0) ^ 365) - 1.0) * 100.0. GSD itself is simply Average Return / Average Days Held. Target Holdings is round(Holdings / %Invested * 100.0). AvgReturn div Turnover is Average Return * (Turnover / 100.0) / 365.0 (note that it actually multiplies by Turnover, despite what the variable name says). LOG(Target Holdings) is the natural logarithm of Target Holdings.

My “prediction” formula, labeled as PREDICTED_OOS_RETURN in the scatter plot in my first post and by ANN_EXCESS_PREDICTION in the other post with scatter plots, is the result of the linear regression of AvgReturn*Turnover and LOG(Holdings) on Ann Excess Launch (the difference between the two is only the use of LOG(Holdings) vs LOG(Target Holdings)). The exact formula I used for ANN_EXCESS_PREDICTION is -34 + 287.3388 * Average Return * (Turnover / 100.0) / 365.0 + 8.0035 * LOG(Target Holdings). Those numbers were found by the regression.

If you create an additional column in the CSV file with that formula, then you can make a scatter plot in Excel with Ann Excess Launch versus that new column. That will give you the same scatter plot as the lower right one in my previous post.

I don’t know how to do linear regression in an easy way in Excel. And it should be used with care, because it’s easy to misinterpret results. When you just want to regress one variable on another, it’s easiest just to make a scatter plot and try to look for a relationship. You can add a trend line, and I think there’s also on option to see the formula for the trend line somewhere.

Hope this helps.

-Peter

24

Linear Trendline Equation: y = m * x + b
m: =SLOPE(y,x)
b: =INTERCEPT(y,x)

This equation assumes that your sheet has two named ranges: x and y arranged in columns, where x is the independent- and y is the dependent variable.
Georg

25

Peter,

Thanks again for sharing your results. You seem to know a lot about this. I have a related question. I don’t know if it is related enough that it interests you or not but here it goes.

There is an option in the Ranking systems for correlation and Reverse Engineer. 4th and 5th down from the left with Factors first and Performance second.

Have you (or anyone) tried either one of these and do you find them useful? It does seem that what you are doing mirrors the intended use of Reverse engineer and correlation (if I understand it at all).

26

Jim,

I’m studying econometrics at the moment, and this turned out to be a great little project to put all the theory into practice :slight_smile:

I never tried the correlation feature, so out of curiosity I just tried it out. It looks interesting indeed, and looks similar to what I did. However, it is limited to max 20 samples, which is really small. Of course you could run it multiple times to cover more samples, but that would not really be the same as using all samples at once. You could get a kind of rolling correlation, but that takes lots of clicking.

On the plus side, you’d only have to do this once for your favorite factor(s), because the numbers for the individual factors do not seem to depend on the set of factors or weights you happened to use in the ranking system.

I have tried the reverse engineering option, but did not have much success with it. I did not spend much time on it. Doesn’t mean it cannot work though.

-Peter

27

pvdb - thank you for this description. The reason for confusion was because I didn’t see where you were calculating compounded GSD. I’m not a statistics whiz but I still don’t believe that you calculated it properly. The problem lies with the simple Avg Profit/Avg Days Held. You are first calculating the simple GSD then converting to annual using a compounding formula. This is not correct. The actual formula (in my opinion) should be:

    [b]Annualized GSD (%) = (1+Avg Profit/100)^(365/Avg Days Held)-1)*100[/b]

When you do this you end up with a graph like this (see attached). Once this calculation is done then we can start looking at the impact of various factors such as turnover, profit per trade, number of holdings, time in market, etc. These should be dealt with using an envelope, not part of the best fit equation. This was mentioned by others. BTW - there is a bias with the GSD calculation as the OOS results make up part of the GSD calculation. I’m not sure how significant it is but will have some minor impact.

Here is the location of the spreadsheet I used to generate the graph:

https://dl.dropboxusercontent.com/u/196977195/r2g1.xlsx

R2G-analysis.gif
R2G-analysis.gif884×495 20.7 KB

28

The correlation is going to be affected a great deal if the model hedges or uses market timing. Good looking correlation but would even be better without market timing or hedging.

BTW do you have a correlation coefficient for that?

29

Steve,

I agree your formula is the correct one. I quickly checked, and the correlation with my (imperfect) version is actually 99.75%. The difference can be significant for some models though. On the other hand, the explanatory power seems to be roughly equal to the other versions of GSD. That is to be expected when the correlation between the different versions is very high.

I don’t know what you mean with envelope.

There is indeed a bias in the GSD numbers because they include out-of-sample results. In all, I don’t think this bias is big enough (yet) compared to other issues like small sample size etc.

Another substantial bias is introduced by using Ann Excess Launch (as remarked in this thread). I did a similar exercise on Return 6M, again using only models with Days Launch >= 180. That means that the returns of all models span exactly the same time frame (6 months). That gave the following list of single variable correlations (with Return 6M). Note that the top 13 (!) of variables are all measures of raw performance, except for 3 year Sharpe and Sortino.

Model 3Y Annualized Return (R2 = 0.4318)
Model 3Y Alpha (annualized) (R2 = 0.4160)
Model 3Y Sharpe Ratio (R2 = 0.3591)
Model 3Y Sortino Ratio (R2 = 0.3286)
AvgReturn * Turnover (R2 = 0.2967)
Ann Excess Inception (R2 = 0.2483)
Alpha (R2 = 0.244)
Model Incep Alpha (annualized) (R2 = 0.244)
Model Incep Annualized Return (R2 = 0.2408)
Annualized Inception (R2 = 0.2408)
GSD (R2 = 0.2328)
Annualized GSD (Steve) (R2 = 0.2314)
Annualized GSD (R2 = 0.2294)
Model Incep Sharpe Ratio (R2 = 0.1999)
Model Incep Sortino Ratio (R2 = 0.1845)
Model 3Y Standard Deviation (R2 = 0.1181)
Model 3Y Correlation with benchmark (R2 = 0.0986)
Model Incep Standard Deviation (R2 = 0.095)
Model 3Y R-Squared (R2 = 0.092)

No longer statistically significant according to t-test:

% Invested (R2 = 0.0813)
Turnover (R2 = 0.075)
Model 3Y Max Drawdown (R2 = 0.0748)
Average Days Held (R2 = 0.0728)
Views (R2 = 0.0707)
Min Stock Price (at purchase) (R2 = 0.0569)
Model Incep Correlation with benchmark (R2 = 0.0476)
Yield (R2 = 0.0461)
Cost (R2 = 0.0406)
Model Incep R-Squared (R2 = 0.0403)
Liquidity (R2 = 0.0370)
Avg Ret Winners (R2 = 0.0166)
Subs (R2 = 0.0138)
Winners (R2 = 0.0135)
Average Return (R2 = 0.0090)
Days Launch (R2 = 0.007)
Max Profit Contribution Single Stock (R2 = 0.0052)
Holdings (R2 = 0.0038)
Model 3Y Beta (R2 = 0.0025)
Target Holdings (R2 = 0.0025)
Avg Ret Losers (R2 = 0.0024)
Drawdown (R2 = 0.0003)
Model Incep Max Drawdown (R2 = 0.0003)
Model Incep Beta (R2 = 0.000)
Trading Costs / Curr Mkt Value (R2 = 0.0000)

I think I’ve tortured the data enough for now. It has certainly confessed to me that backtested performance is highly correlated with actual performance in the past 6 to 12 months. Now let’s hope it holds up going forward…

30

pvdb - I know I’m driving you crazy with my pickiness :slight_smile: Some of the GSD numbers are off by as much as 10%-15%. I learned a long time ago with my engineering background that when you start making approximations here and there all of a sudden you can very quickly find yourself looking at mud instead of a clear picture.

envelope - instead of trying to incorporate number of stock holdings into the equation, it is better to create an envelope of uncertainty around the best fit line. Perhaps with the correct equation for GSD we can now start to explore the PDF of %profit and days held. With this knowledge it is conceivable that a distribution about the best fit line could be constructed. Or maybe this is just my imagination running wild.

Anyways, you’ve caused me to embark on my own journey. http://stockmarketstudent.com/stock-market-student-blog/pre-versus-post-launch-stock-model-performance

It may be a long and perhaps unsuccessful journey though.

Steve

31

Steve,

I’m all for your version of annualized GSD, but in this one very particular case it didn’t make a noticable difference. So the level of muddiness in this particular puddle didn’t change much. But going forward it’s definitely best just to use your version.

Linear regression is capable of handling multiple variables at once, and there is also a lot of theory about computing the uncertainty of the coefficients etc. In fact, you can derive the distribution about the best fit line with that theory. However, any attempt will necessarily need to make assumptions about the distribution of the data itself. As far as I know, there is no single known distribution for stock returns, and therefore also not for portfolio returns. With very large sample sizes the exact distribution is less important (because of the central limit theorem), but we only have a very small set of models to work with.

I’ll be following your posts and hopefully we can learn more going forward.

Peter

32

Steve,

I am just playing around with the data a little - around ‘naive manager selection’ methods I might have used 300 days ago. Not trying to get into the Harvard Medical Journal. :slight_smile:

Here’s more ‘random’ tidbits. Don’t know that they will much change what I’m doing…but -

…There are 36 or so R2G’s with over 300 days since launch. They average 335 days since inception. They average 13 holdings each. If no holdings overlap , that’s 468 holdings. Lets assume half of all holdings overlap to be conservative (234). The average annualized return since launch of these 36 R2G’s is 38% (the average of systems with 335 to 376 days since launch is 34.5% and the average of systems with 307 to 335 days since launch is 41% - so not a huge difference).

50 random runs of 234 stock sim’s (half monthly and half annual rebal, with var. slippage) returns over the same ‘average’ trailing 335 days yields an average return of 21% with a Stdev of 4.2 between the runs. Just annual rebalance is around 24% with Stdev around 3.3. So, to my eyes there is only a very, very low chance (somewhere in the ballpark of 1-2% say) that R2G outperformance to date is mere chance. R2G’s appear to contain collective real alpha as a total group pre-tax and pre-fee if people can trade them at the sim. settings for slippage and fill prices.

For someone trading a large port, tax-free this is pretty good news. Potentially.

However, I trade almost all my money in a taxable account. Almost all P123 gains are short-term. And so post tax (with state and federal taxes, I pay roughly 40-50% for St. cap gains, all-in, depending on the year). So…for people like me, R2G’s and Random stock selection with no rebalance are roughly a push in total return over the first 300 days. So…this is the long-term hurdle R2G’s have to beat. So…basic conclusion still the same - not sure it’s gonna be worth it on an absolute basis unless a person has real manager selection skills. Or more strat’s that are tax efficient evolve. Even a one time per year rebal system could cost me 25% or more to taxes if it has 100% turnover, all long-term gains.

But…for me it’s as much about managing risk and peak DD’s. So, another big question is can they do better on a risk-adjusted basis long-term. And by how much? That will only be shown by blended performance of hedges and timing over some pretty long cycles (5-10 years).

I know post-tax returns on sim’s have been kicked around. I would love that feature.

Best,
Tom

33

Tom,

I like your statistics even if Harvard has not seen the light yet. I want to emphasize a point that you have alluded to because I have been thinking a lot about it. In order to obtain the same results as the ports you would have to have some stocks with a high concentration (some increased in risk). Doing the math, I think if a stock is recommended by 2 ports you have to double-up on that stock. If it is recommended by 3 ports then you have to triple up etc. So more than likely, if you had actually followed all of the ports one of 2 things would have happened. 1) You would follow the ports exactly, purchasing more stock each time it is recommended. In which case you probably would have been very concentrated in a few stocks at any given time. or 2) You would have bought the stock the first time it was recommended and at some point stopped buying more when it is recommended again. In this case, you would not be as concentrated in a few stocks but your performance would drop.

Perhaps, some might debate this. It is my experience and others have posted that the stocks that are recommended by more than one port perform better than the stocks that are recommended by just one port. This can be tested in the sims to some extent.

I find this to be an interesting general problem. I think it is one important reason the retail investor does poorly watching TV talking heads. If he does what Cramer recommends but then does not double-down when Fast Money recommends the same stock (even though he usually buys some stocks after watching that show too), then he is almost guaranteed to under-perform both Cramer and Fast Money over the long term.

In statistics this is the Monty Hall problem, also I have 2 children one is a boy or I have 2 Aces and one is a spade problem.

34

Tom -
{ shush…Quiet }
Defensive Sectors (Tax Smart)
Growth and Income (Tax Smart)
Pure Income (Tax Smart*)

{ I’ll slip you the money later when no one is looking. }

35

Or you just emigrate to the Netherlands, where individuals do not pay capital gains tax at all :slight_smile: Just 15% dividend tax, and an annual 1.2% tax on total assets.

36

Steve,

I like what you’re trying to do.

As for me…I’ll still pay a lot on long-term gains and dividends. So…systems still need to be better after this.

Currently:
The distinction between ordinary and qualified dividends is scheduled to expire at the end of 2012. Absent further legislation, dividend income will revert back to being treated as ordinary income subject to the ordinary income tax rates.

So…I’ll be paying the same hi rates on the div’s here. And only boosting after-tax returns by 25% or so on the l-t gains.

It’s not an easy challenge. Low to mid 20% AR is the best I can do on large cap, 20 stock plus, yearly rebalance sim’s so far. 18% or so on 50 stocks. With reasonable number of rules. They still will have market level DD’s.

Best,
Tom

37

Pvdb,

I like it. What’s the warmest part of the Netherlands? I’m in. Why not. Wait…1.2% on total assets. Hmmm…Need to think about that. How’s the cost of living?

EDIT: I WAS WRONG. YOU ALL ARE RANKED AS THE 4TH HAPPIEST COUNTRY. I’M THERE.
http://www.iamexpat.nl/read-and-discuss/expat-page/news/netherlands-fourth-happiest-nation

:slight_smile:

38

Tom - I’m not sure where you got your info…

“The American Taxpayer Relief Act of 2012 (signed on January 2, 2013) made qualified dividends a permanent part of the tax code but added a 20% rate on income in the new highest 39.6% tax bracket.” http://en.wikipedia.org/wiki/Qualified_dividend

Regardless of what tax bracket you are in, you are looking at a reduction of at least 50% in taxes for long term gains. I believe annual return has to be at least 50% more for a tax smart portfolio, probably a lot more when you figure in the high turnover of most R2G models. (That assumes that one makes a profit of course :slight_smile:

Steve

39

It seems to me that what Tom and pdvb are saying are both playing out. R2G ports over 180 days as a whole are delivering alpha. The number of believers of quant investing on this site supports that; we wouldn’t be here if this approach wasn’t delivering alpha, and R2G’s are arguably some of the best of breed. So its not hard to believe that R2G’s with monster back tested numbers tend to outperform out of sample (setting aside questions of benchmark, survivorship bias etc), because the overall approach has been proven to satisfaction for most of us, and these models are some of the best within that approach.

But we can all see that, so far, there’s also a couple ‘big name’ p123 user-designers who’s R2G’s have underperformed, esp in light of the market action since R2G launch, as well as the R2G’s who have hit it out the park. This seems consistent with Tom’s analysis, that there is huge variation due to small things ~ randomness.

Since the big number R2G’s are all basically built on core ranking systems focused on less liquid small cap - value - momentum situations, and mostly hold a pretty small number of these, 3 or 4 stinkers will crater out of sample performance; equally, catching 3 or 4 rockets will really juice performance. The same stock could be both.

FU for example. R2G’s catching it on the up were laughing, R2G’s jumping in near peak were crying, and there was not much time in between. While an extreme example, the less liquid / rocketship R2G models tend to choose stocks with FU’ish elements… of which some will continue to blaze and some will rollover. So some R2G’s will way underperform, and some will way overperform, and that is probably mostly due to chance. Although we can’t prove it. And its still early.

So good luck to anyone trying to pick out the ‘best’ R2G model, esp the future biggest hitter, coz a big dose of that’s what you’ll need to a priori identify the future winner out of the R2G’s with big backtest numbers from a pedigreed designer. Stylistically they’re pretty similar. Not that this is consolation to those whose models underperformed out of sample, or will be remembered by those who’s models overperformed!

I suspect also that pdvb’s main conclusion, that R2G’s are solidly delivering, will weaken somewhat (but not disappear). This is mostly because

  1. The market conditions since R2G launch are as friendly as possible and the R2G’s have mostly delivered, but R2G performances relative to market performance (1.5-3x) is nothing like the historic backtested ratio of R2G performance : market performance (3-15x ++). The last year could be an upper bound for R2G : market outperformance. The hiccups of the last 60 days have seen deterioration in a lot of R2G model performances (deterioration in the sense of underperforming the market, not just a slowing in out-performance). Most of the newer launches are not sporting annualised returns that look near as good as those launches mid last year.

  2. The market timing systems are blunt, have short back test histories etc, and could easily underperform out of sample worse than the ranking systems do; we haven’t seen much thrown at this part of the systems yet

I also doubt many subs are getting real world numbers like the R2G’s, unless they are in the very liquid R2G’s. As people noted with STRT awhile back the slippage on stocks concurrently found in several R2G’s can be way up there.

One thing I enjoy a lot on these boards is the depth of analysis / quality of contribution, which while it so often brings us back to the beginning (Does this really work??) we get back with a lot more numbers :slight_smile:

Justin

40

@Steve. Thanks. I guess that’s why I use to pay an accountant (but now use Turbo Tax). I just cut and pasted from the first link I saw to a tax site. But the law was changed. You’re right I think. Haven’t done my 2013 taxes yet.

I pay (at least) 10% Cali taxes on top of 39.6% Federal taxes. That 10% State tax is deductible (so I get 3.96% back), but still creates a very hi marginal tax rate (around 46%) most years. It’s all based on portfolio earnings, so varies a lot. And sometimes I get tax loss carryforwards. So…it’s not that straight forward.

I think long term gains are coming in around 15% federal and 10% state. About 23.5% total. So…I am saving, at most, in my best earnings years - around 22.5% on systems with all long-term gains over systems with all short-term gains.

So…I have to make about 13.4% to earn 10% after tax if all long-term gains. But 19% or so if all short-term gains to earn the same 10%.

So…long-term gains can be multiplied by 1.4 or so to get to short-term gain system equivalent. Right?

My only point is…everyone’s tax situation is different, but not many people will have to pay more taxes than this. So…at most that’s the multiplier. So…L/T systems still have to be better after adjusting for tax differences.

I could be wrong on the tax amounts. I just plug it all in to Turbo Tax. I think the general point still holds.

Best,
Tom