Factor Momentum

[Jrinne]

Victor,

Edit: I question the significance of just these 2 factors due to the multiple-comparison problem with 40 data points (i.e., none would be significant with the Bonferroni correction). But if you tested 20 different factors and found that all or most had positive correlation for the first few weeks that would be interesting, I think. Maybe use a Fisher's Exact test on 20 factors (categories being 'positively correlated first week' or 'negatively correlated first week'). Just a thought of something that could be looked into. But not enough data in my post for any conclusions, IMHO.

Thank you for that reference. I always like to take the methods of papers and use them with P123 data.

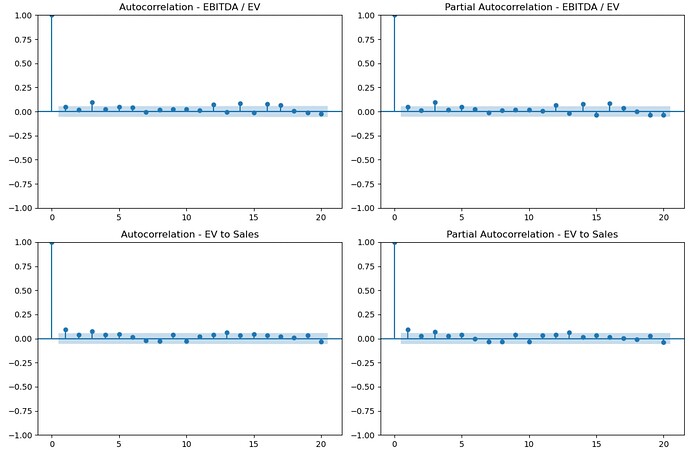
This is the autocorrelation of the excess returns of the top bucket (30 buckets, 2000 - 2024 weekly excess returns relative to the easy to trade universe) for the factors in the screenshot. I leave it to each members to form their own conclusions or test it themselves with their own factors:

Just for those who wish to check my code (or use it). Corrections welcome:

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

(#) Specify the file path (replace with your actual file path)
file_path = '/Users/your_username/Desktop/autocorrelation.csv'

(#) Read the CSV file into a DataFrame
df = pd.read_csv(file_path)

(#) Convert the 'Period' column to datetime and set it as the index
df['Period'] = pd.to_datetime(df['Period'])
df = df.set_index('Period')

(#) Plot autocorrelation and partial autocorrelation with significance bands
fig, axes = plt.subplots(2, 2, figsize=(12, 8))

plot_acf(df['EBITDA / EV'], lags=20, ax=axes[0, 0], alpha=0.05)
axes[0, 0].set_title('Autocorrelation - EBITDA / EV')

plot_pacf(df['EBITDA / EV'], lags=20, ax=axes[0, 1], alpha=0.05)
axes[0, 1].set_title('Partial Autocorrelation - EBITDA / EV')

plot_acf(df['EV to Sales'], lags=20, ax=axes[1, 0], alpha=0.05)
axes[1, 0].set_title('Autocorrelation - EV to Sales')

plot_pacf(df['EV to Sales'], lags=20, ax=axes[1, 1], alpha=0.05)
axes[1, 1].set_title('Partial Autocorrelation - EV to Sales')

plt.tight_layout()
plt.show()

Jim

[yuvaltaylor]

This is not scientific at all, but I thought I'd relate my own anecdotal experience with factor momentum. I broke my factors down into seven general categories and created a way to change their weights depending on factor performance over the last nine months or so. The end result was so much turnover that it seriously damaged my performance.

I came up with an alternative a little while later, and that is to use a few "flip factors" in my ranking system. These are conditional factors that flip between a value factor and a growth factor depending on whether the recent performance of $SPALLPV (S&P 1500 pure value) is better than the recent performance of $SPALLPG (S&P 1500 pure growth). Many of these conditional factors backtest better than either of the included factors alone. This is a very lagging indicator, but because the trends tend to last a while, it seems better than nothing.

[Jrinne]

@Jrinne

But if you tested 20 different factors and found that all or most had positive correlation for the first few weeks that would be interesting, I think. Maybe use a Fisher's Exact test on 20 factors (categories being 'positively correlated first week' or 'negatively correlated first week'). Just a thought of something that could be looked into. But not enough data in my post for any conclusions, IMHO.

I decided to do this with a ranking system that has a modest number of factors most of you would recognize. Many factors are from the core system. You could test this yourself with all of the core system factors or your own ranking system and factors you know and presumably use. You have the code and the P123 downloads to improve on this small study. It could definitely be improved upon but I thought it had enough factors to be interesting.

Modifying the autocorrelation code above, I found 18 out or 31 factors had a positive correlation with a lag of one week. I used the excess returns relative to the easy to trade universe.

Results and code are below. In summary, using 31 factors may not have had enough statistical power, but with 31 common factors I was unable to reject the null hypothesis of no correlation (positive or negative) for the first lag (p-value = 0.15). Also I wonder about the practical significance of only 18 out of 31 factors showing positive correlation for the first lag—over period of 24 years--even if a larger study did show statistical significance.