Fewer parameters make better models.

Manage
1

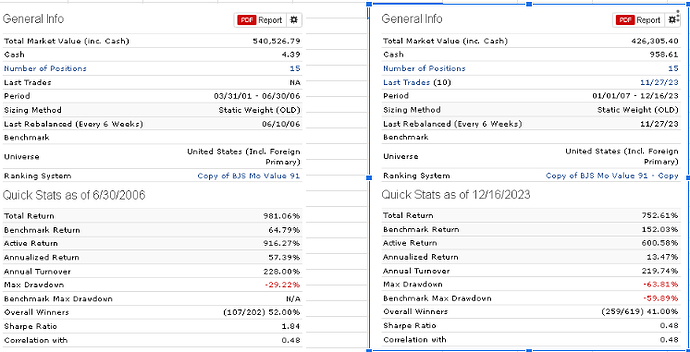
This is a follow up on view thread http://www.portfolio123.com/mvnforum/viewthread_thread,6973_offset,40 when I suggested that model designers state the number of parameters in their R2G models, but nobody supported that idea. Now we see R2G models with over 150% annualized returns and one wonders how many parameters the models have to produce such high returns.

Below is condensed from
http://gestaltu.com/2014/02/toward-a-simpler-palate.html

Performance decay occurs when the performance of a systematic trading strategy is materially worse in application than it appeared during testing.

Degrees of freedom in a system (the number of independent parameters in the system that may impact results) relates to the counterintuitive notion that the more independent variables a model has – that is, the more complicated it is in terms of the number of independent ‘moving parts’ - the less reliable a back-test generally is. This is because more independent variables create a larger number of potential model states, each of which needs to meet its own standard of statistical significance. A model that integrates a great many variables seems like it would be robust; to the contrary, it is likely to be highly fragile.

A particular model design had no less than 37 classifiers, including filters related to regressions, moving averages, raw momentum, technical indicators like RSI and stochastics, as well as fancier trend and mean reversion filters like TSI, DVI, DVO, and a host of other three and four letter acronyms. Each indicator was finely tuned to optimal values in order to maximize historical returns, and these values changed as when optimized against different securities. At one point a system to trade IWM (iShares Russell 2000 ETF) produced a historical return above 50% and a Sharpe ratio over 4.

These are the kinds of systems that perform incredibly well in hindsight and then blow up in production, and that’s exactly what happened to the IWM system to time US stocks which lost 25% in a few weeks.

The problem with complicated systems with many moving parts is that they require one to find the exact perfect point of optimization in many different dimensions – 37 for the IWM model.

It isn’t enough to simply find the local optimum for each classifier individually without considering its impact on the other ingredients. That’s because, in most cases the signal from one classifier interacts with other classifiers in non-linear ways. For example, if you operate with two filters in combination – say a moving average cross and an oscillator – you are no longer concerned about the optimal length of the moving average(s) or the lookback periods for the oscillator independently; rather, you must examine the results of the oscillator during periods where the price is above the moving average, and again when the price is below the moving average. You may find that the oscillator behaves quite differently when the moving average filter is in one state than it does in another state.

To give an idea of the scope of this challenge, consider a simplification where each classifier has just 12 possible settings, say a lookback range of 1 to 12 months. 37 classifiers with 12 possible choices per classifier represents 6.6 x 10^18 possible permutations. While a quintillion permutations may not seem like a simplification, consider that many of the classifiers in the 37 dimension IWM system had two or three parameters of their own (short lookback, long lookback, z score, p value, etc.), and each of those parameters was also optimized…

There is another problem as well: each time a system is divided into two or more states you reduce the number of observations in each state. To illustrate, imagine if each of the 37 classifiers in the IWM system had just 2 states – long or cash. Then there would be 2^37 = 137 billion possible system states. Recall that statistical significance depends on the number of observations, so reducing the number of observations per state of the system reduces the statistical significance of the observed results for each state, and also for the system in aggregate. For example, take a daily traded system with 20 years of testing history. If one divides a 20 year (~5000 day) period into 137 billion possible states, each state will have on average only 5000/137 billion=0.00000004 observations per state! Clearly 20 years of history isn’t enough to have any confidence in this system; you would need a testing period of more than 3 million years to derive statistical significance.

As a rule, the more degrees of freedom a model has, the greater the sample size that is required to prove statistical significance. The converse is also true: given the same sample size, a model with fewer degrees of freedom is likely to have higher statistical significance. In the investing world, if one is looking at back-tested results of two investment models with similar performance, one should generally have more confidence in the model with fewer degrees of freedom. At the very least, we can say that the results from that model would have greater statistical significance, and a higher likelihood of delivering results in out of sample that are consistent with what was observed in simulation.

1 Like
2

I too have been concerned about the use of multiple (particularly technical) rules to achieve fantastic returns. I have also been concerned about the way that fuzzy logic works to combine the different factor parameters to result in a highly “tuneable” set, but without having much predictability about the future.

I have been attempting to boil things down into single equations that make logical sense, and show a degree of innovation and sophistication beyond what most will have thought of. To win at trading, one needs to be in the top 1%, and that means being exceptional.

I am happy to say that my new Ultra Extreme Trader has a ranking system that contains 9 factor parameters, but before envious model designers get gung-ho with their optimisers, I can tell you that 8 are custom formulas and there are one or two masterpieces in there that blind optimisation will never reproduce.

Almost exactly 1 year ago I launched precisely 4 model portfolios, and they have all greatly exceeded the market performance since.

3

Geov, btw I did backtest your market timer last year on the cac40 and the nikkei225. If you’re curious, drop me a line and I’ll publish the results.

4

Well said and it is my belief that you are probably right.

I have been interested a fine point. It is my belief that there some optimizations the are not harmful to future returns while some optimizations are harmful. For example, I thing changing the weights of factors without adding new factors is probably not harmful.

I cannot prove this but consider this thought experiment. Take 3 factors and assign random weights to these factors. Then use Steve’s optimizer on these three factors. On what basis do you believe the optimized ranking system is worse. After all, the optimized weights could have been selected randomly in the first place. You really can’t argue the optimized ranking system will perform poorly just because it did well in the past. You would have to have a mechanism or reason the optimization might make things worse. While I don’t believe optimizing always hurts future return, it is easy to imagine an example where it would.

Let’s assume you optimize with hedging a leveraged inverse ETF. Let’s assume your timing is heavily optimized and much of it is not really effective and the backtest is improved by chance. This can be very damaging because randomly buying leveraged inverse ETFs (based on an ineffective strategy) is a losing proposition based on compounding, volatility loss or whatever you call it.

Anyway, I just wanted to start a discussion on what types of optimization might be okay and which types probably are not okay if that interests anyone.

Thanks.

5

I’m more concerned about the robustness of technical factors.

Tweedy Brown’s What Has Worked says stocks with price declines outperform. They seem to be looking at longer term price declines. Numerous studies show that momentum works. I hear about models that look at medium term outperformance and short term underperformance (is this a “pull back” system?). So if we say mean-reversion is the opposite of momentum, I’m to look at stocks with long term mean-reversion, medium term momentum, and short term mean-reversion? Seems to me that what is considered long, medium, or short term can shift over time, and therefore break the system. Sometimes resulting in whipsaw.

I wonder if model complexity is necessarily bad. Say you have lots of factors, but each factor is strong when used alone. I would think that using 2 strong factors together is better than 1, in case one of them stops working, especially if those factors are independent and orthogonal (not 2 very similar valuation factors for example).

Many R2G’s show sensitivity analysis: sensitivity to # of stocks, different liquidity requirements, etc. This is good. But they are all for the same ranking system. What I would be curious to see is what happens if you remove a single node at a time. I don’t think this has ever been shown.

The Piotroski F-score has 9 items. Is this fragile? My guess is no. You can explain the rational behind each one. But if you had 9 technical factors? I’m probably biased but i feel like justifing 9 technical factors would be harder.

I guess my concern is more with factor reversal than factor decay. And with permanent reversal compared to temporary. ROA higher is better. In what universe would this permanently reverse? Perhaps if high ROA stocks are systematically overpriced. So you combine it with a valuation factor. So I guess if you can reason these things through I’m more likely to stick with it during periods of underperformance.

Greenblatt is a rich hedge fund manager. He has a team of quants, right? He has lots of resources. Then why does his “Magic Formula” only have 2 factors? Can’t he easily find a 3rd or 4th? I think it’s partly because he wants to market it as a value-weighted “index”, partly becauase he wants so pick a large number of stocks, and maybe partly for robustness.

6

Aurelaurel, I have done this too for a number of world markets, in local currency and in USD.
Had one been invested only during the periods when Best(SPY-SH) was long SPY (as listed in Table 3 of iM-Best(SPY-Cash) Market Timing System) and stayed in cash at all other times, then the annualized returns from all markets would have improved on average by about 10.8%. Furthermore the maximum draw-downs would also have been significantly lower.

Better Returns from World Markets with iM-Best(SPY-SH) Market Timing System.
http://advisorperspectives.com/dshort/guest/Georg-Vrba-131004-World-Markets-Timing-System.php

7

Greenblatt apologized for the lack of robustness of his two factor formula and said he learned it worked best in only a certain timeframe. He has since revised it. In effect, he admitted that a model will not perform well in all time periods. An honest man. Proves that it is best to use different models for diversity.

8

OK, so too many independent variables will cause a system to fail out of sample. So how many are too many? Lets test some of the old public ranking systems that were available prior to the beginning of the recession in 2007, and see how many failed out of sample since 3/09/2009 (They all pretty much failed during the recession, but then so did everyone else’s). I ran the ranking system performance from 03/09/2009 through yesterday using a universe filter of ADT> $200K and Price >1. Here are the results:

The first one is Bompusrank3_v0.2; This system has 21 factors & functions and achieved a 74.5 annual return out of sample.

Next, Filip’s Super Value; this one has 25 factors and functions and achieved a 65.8% annual return out of sample.

Next, Dan’s Excellent Only Optimize; this system has 15 factors and functions and achieved a 49.4% annual return out of sample.

Next, TopPort123Factors&Formulas; This one has 37 factors and functions in 7 composite nodes and achieved a 37.1% annual return out of sample.

Next, BJS Mo Value; this one has 28 factors & functions with 6 composite nodes and achieved a 34.2% annual return out of sample.

Next; ValuMentum; this one has 29 factors & functions in 3 composite nodes and achieved a 30% annual return out of sample.

I guess I shouldn’t have invested in the stocks that were high ranked by these systems since they were sure to breakdown because they had too many variables. It must have been pure chance that I made a LOT of money from these systems over the years and was able to retire early at age 62. I’ll be much more careful in the future!

Denny :sunglasses:

PS: one of my private systems I made up by combining 4 other great systems in 2009 contains 50 factors and functions in 4 composite nodes. It achieved a 92.9% annual return since then using the above filters. I am sure that it will fail any day now. :smiley:

9

Denny, I think you are ironic here :wink:

My short experience is: within the ranking a lot of variables should not hurt, what makes modells shaky in real time are to much the buy and sell filters that filter out to much stocks.
Also it is not so much the amount of variables (ranking, buy and sell filters) but how much “degree of freedom” they “eat up”.

For Example “EPS%ChgPQ > 0” dos not “eat up” as much degrees of freedom (a Model needs degrees of freedom to differentiate between noise and something real) as “EPS%ChgPQ > 150”.

Also (I know much of you have a different opinion on this): I like models that Show strong “correlation” (or better: “swings
up and down with the market”) with the market, because if you cannot see that “correlation” in the real time Phase, you know something is wrong, if you have a System that does not show correlation it is much harder to see that it is “blowing up” real time.

The stuff I trade mainly for my own Portfolio is very, very simple:

3 Month System with a well-known ranking System of olikea, It trades 100 Stocks:

AvgDailyTot(20) < 500000
AvgDailyTot(20) > 25000
EPS%ChgPQ > 15
(close(0,#spepscy)>ema(75,0,#spepscy)) or (close(0,#bench)>ema(75,0,#bench))

Sell:
(close(0,#spepscy)<ema(75,0,#spepscy)) or (close(0,#bench)<ema(75,0,#bench))
Rank < 80

You will not belive it, but slippage with a 212k Portfolio (so far!) is positive using GTC orders.
I put in the 30-50 orders every 3 Months with favorable Limits and after a week I check them
and 80% of them are filled, the rest I tweak and move to the last Close Price and after some more
tweaking the Limits in another week all of them are filled.

The vola of the Overall System is very, very low, it moves with the market yes, but for example it
had a DD of 3,5% when the market had one of almost 6%.
The vola of the single stocks is high as hell (very often -20% Stocks or + 30% Stocks on
a single day): BUT → with 100 Stocks you “dice” every day 100 times which leads
to a great overall low volatility.

Best Regards

Andreas

10

Georg,

I share your bias for ‘simple’ is often better.

Having said that…There are countless ways to build and test effective systems. Simply counting parameters does very, very little. As Judgetrade points out - not all rules are created equal. Some parameters may have zero impact on backtest results - but the designer thinks they make the system more stable and/or they make me more comfortable trading it, or offering it to others (i.e. maybe 3-4 ways of measuring value instead of one…to get at a more stable measure, less subject to any reporting or data errors - or trying to cut out some companies I just don’t want to own - no matter what my backtests show). So…some rules I add will lower performance in backtests.

Some rules may weed out 10 stocks. Some may weed out 2,000 stocks. Both are one parameter. Some rules may come from an academic study with a 100 year backtest across thirty markets. Some may be obscure technical rules that I’ve never seen before and find in parameter testing. I’m much more cautious with the second than the first - in both cases. But…Designers include additional rules for many, many reasons. The only goal here is stable out of sample performance over long time periods. So…A key point in backtesting with all rules is a) how much of the system return is being driven by any single rule and b) how much of a difference do extreme weight variations in that rule make and c) how ‘unusual is that rule.’ How much do I understand why and how it works?

So…Simply counting number of parameters can be ‘forced’ to be reported or not, I don’t know how I feel - but my guess is that, on a stand alone basis, it’s going to add very, very little value (most likely) on it’s own and could have negative consequences (i.e. forcing designers to remove well designed ‘safety’ rules). However, maybe it will allow studies on parameters and OSS down the road. So…I’m fine offering this additional data point. I’m all for the transparency. It will be interesting little experiment. But…I would be more likely to limit this to high end memberships as interpreting this data point is fairly complex. However, I doubt it will ‘pass’ the community. Just like ‘batch processing’ of sensitivity studies. I like that idea as well. But…all of these are subject to abuses and negative consequences. Ultimately people are betting on designers.

Other examples:

I know a team day trading their own money in only long-short SP500 and nasdaq future contracts (open orders in the morning daily, adjust position sizes intraday and close out before market close daily). 1 system. Intraday trades only. 1 million lines of code plus. Over 7 years out of sample. More than 50% annual return over 6 years on his own money. (He’s a leading University finance professor and just trades his private account as well as the accounts of the people who code his stuff). So…yes, simple is better. But he’s got over 1 million rules. It’s worked over 7 years now (he showed me his interactive brokers statements). There is zero chance what he’s doing is ‘luck.’

And…All you have to do now is look at R2G systems 1 year out. There are many that have done great out of sample. Several of those are clearly very complex with a lot of rules and very few holdings.

Many P123 users have been trading small portfolios of highly complex systems for a decade (or more) now with, as Denny points out, great results.

In my own (admittedly more limited) case, I have several ‘complex’ versions of systems that have far outperformed their more simple counterparts over a year plus out of sample (I put money into the stripped down min. parameter versions and the more optimized versions, because I didn’t / don’t know which would do better out of sample in any roll forward period).

Best,
Tom

11

Denny,
The 5 year bull-market started on 3/9/2009, when the S&P hit its lowest level. All models would have done well since then. So this is not really a test. Just holding SPY provided a 25% annualized return without any trading effort at all. The systems you refer to are all bull-market systems which imploded during the last recession. As you say “They all pretty much failed during the recession, but then so did everyone else’s.” So if systems are only going to work during bull-markets then we might as well forget about P123 and R2G and stay with buy-and-hold, and only get out of the market prior to recessions.

This bull-market is not going to last forever, it will be interesting to see performance of the models when the market climate changes.
Georg

12

Geov,
basically, I agree.
BUT, the first thing I am looking at when I look at a R2G model is the time frame of 2008/2009 and 2000. These were disaster years for the stock market. I want to know how the model did during those periods. If it did decently well, I may be interested. If it collapsed, no thank you.
There are some models that did well during those times (and not only because of “market timing”).
Werner

13

Georg,

What might be fun/interesting is to push the thinking forward into some more specificity on ‘good complexity’ versus ‘bad complexity’ - things such as - first a) how to classify rules into ‘types’ (say on a ‘complexity scale’ from 1-10) and then b) how to make better choices for choosing portfolio dollar allocations based on total system ‘complexity’ based on the various ‘types of parameters’ and their complexity type.

Might be interesting learning exercise / discussion? How would we create a ‘parameter’ complexity scale for single rules? If testing factors on a stand alone basis…rank on elements like:

  1. Fewer than 1000 stocks pass the rule. 0/1
  2. The annual (AR%-AR%Bench)/Downside Deviation of the best year of the rule - the worst year of the rule is ‘too large.’ 0/1.
  3. If vary the ‘setting’ (weight or numerical value) on the rule by 20% or more, see more than a 20% change in annual system alpha. 0/1.
  4. If vary the ‘setting’ (weight or numerical value) on the rule by more than 50%, see more than 50% change in annual system alpha. 0/1.
  5. Rule cuts peak DD by more than 10%/yr. 0/1.
  6. Rule cuts peak DD by more than 20%/yr. 0/1.
  7. Rule has fewer than 100 transactions / factor in backtesting. 0/1.
  8. Rule is based on statistical relationship only not on ‘common sense’ underpinning that has long-term research basis, that I understand and get and that has been widely written about. 0/1.
  9. Rule boosts AR% or alpha by more than 5% on underlying universe.

I just made the value up…but the idea is that…something like that becomes a scoring system a designer can use…a modified ‘Piotroski’ style sum of scores gives the parameter ‘complexity.’ The parameter complexities are then summed to create total system complexity rankings.

Might be interesting topic?

Best,
Tom

14

Sometimes, I use a pretty tight screen to pre-qualify the group of stocks to be ranked, in which case, a very small number of ranking parameters can be fine; I even use one model in which I have a single-parameter sort, which can be executed as a one-factor ranking system in sim or a “quick rank” in screener. Other times, I screen leniently (not so much to identify potential winners but more to eliminate potential dumpster fires) and run those results through a more comprehensive ranking system.

Use of many modelling parameters can do two important things for you that cannot be done with less parameters:

  1. Factor diversification can help mitigate the risk of the inadvertent mis-specified model; i.e. where a particular numeric relationship (factor or formula) often tells stories different from what you think it tells. One example might be the sales decline that is not telling you about bad business trends but is instead telling you about the elimination of a money-losing business and consequent increase in profitability. Another example might be the strong cash flow growth that isn’t really telling you about potential increase in shareholder wealth but is instead signaling you about insufficient capital investment and the likelihood deteriorating profitability going forward. Not only is it impossible for any single factor to tell you everything you need to support an investment decision, it’s not even possible for any single factor to consistently tell you what conventional wisdom suggests the factor ought to be telling you. A constellation of factors enhances relating to a particular theme enhances the probability of a model being able to override aberrations here and there and more effectively assess companies.

  2. Use of many factors (particularly when they reflect stylistic diversification) also opens the way to entire classes of stocks that cannot selected by more focused models. It’s a distinction between the generalist versus the specialist. When you trim down to a small number of factors, you’re going the specialist route. In such cases, you are no longer able to say “I want to make money in the market.” You’re instead saying “I want to make money in the market but that’s not so important to me as the desire to make money in the market this specific way.” Also, by limiting the number of factors, you’re in effect saying “I only will consider companies that are “excellent – spectacular – at this small number of things.” And considering that may people use just five stocks, and most probably 30 or less, we necessarily have to be talking about really extreme excellence (that being the only way a company can get a high enough rank to make such a model). There’s nothing wrong with that. But there’s also nothing wrong with generalists; companies that may not be spectacular in any single area but pretty good in many respects. Disqualification of the latter is not always a good way to go.

Both sets of considerations are likely to diminish simulated performance. When predicting the past, we (or at least the database) already know with absolute certainty who the biggest winners were. So the way to spruce up such a prediction is to hone in to the extent one’s detective skills permit on the traits that were held in common during the sample period(s) by those winners. Models with a lot of parameters tend to dilute that effort and, hence, reduce simulated alpha, etc. But it’s a very different ballgame when we turn 180 degrees and look to the future, where nobody and no database knows who the winners will be and what sorts of traits they’ll share.

15

There are three things that I do, to address this issue, a bit differently than what’s being talked about. Along the line of Marc’s point, I think of what factors bring more statistically independent views of a candidate stock or trade setup.

First, when developing a system I think of factors in eight different categories:

  1. Company related (financial statement stuff unique to the company)
  2. Price (and price derivatives e.g. moving averages, RSI, historic volatility, valuation etc.)
  3. Volume
  4. VIX (independently priced option market)
  5. Broad Benchmarks (stock can’t be major component e.g AAPL is > 10% of QQQ)
  6. Analysts (independent people analyzing the same or privileged data)
  7. Intermarket pricing (bonds, commodities etc. are independent competition for capital)
  8. Insiders (privileged information)

I group every factor and trading rule into one of these categories and count up the number of CATEGORIES not factors (never more than 8). If you’re familiar with principal component analysis, these become the principal components. I focus on the essence of what I’m trying to screen out within each category a “theory of the rule”. Often similar rules (e.g. 4 or 5 different valuation metrics) can be simplified without much impact.

Second, I try to have 100 (but at the very minimum 30) TRADES per category. This is just statistics… 100 can detect 2 sigma (95.4%) events (.045*100 = 4.5 instances).

Third, I spend alot of time in excel pulling months out-of-order and trades out-of-order (monte carlo) to understand what happens if the system performs like the past but in different sequences.

For example if I was using Balanced4 I’d group the ranking:

  1. Company (EPS Consistency, Industry Leadership)
  2. Price (TechRank, Valuation)

I think of this as 2 not 17 “risks of curve-fitting”. If I add a benchmark timing and volume rule, there would be 4 categories overall. I would want to see at least 400 trades independent of time. I would then put the 400 trades in an excel “shoe box” and pull them out in different order to create “synthetic years” to see if things hold up.

Factors come and go over time but basic value, momentum and small cap continues to be recognized as anomolies by even the EMH hardcores. I recently added #AnalystsCurFY < 4 to a sim fishing in the Russell 2K and it was detrimental over the long term (less stuff to buy) but helped TTM tremendously. Makes sense since this Bull market is getting a little long and capital is looking for more knooks and cranies. Like FCEL, BLDP and PLUG that have tripled in the last few weeks on no real changes to financials!

16

I would be very interested to know Denny how these system have performed from 2014 to 2023? :slight_smile: Still have the RS from way back?

17

I tried to find them. I’m not sure if its the exact same RS that you tested. I set some minimum requirements as to the number of stocks, and the universe, turnover, and liqudity, just to make sure it was not tilted to the extreme.

image
image752×1571 174 KB

image
image746×381 43.3 KB

Besides one (Dans), this was not impressive.

18

I can fully agree with this statement: As a rule, the more degrees of freedom (more factors with regards to linear models/RS) a model has, the greater the sample size that is required to prove statistical significance.

However, I like to analyse my RS based on ‘The Bias-Variance Trade-Of’ nicely described by prof. Trevor Hastie in ‘An Introduction to Statistical Learning’

‘Variance refers to the amount by which f^ (a function that estimates your target variable), would change if we estimated it using a different training data set’. In our case a universal different training set can be achieved by bootstrapping your dataset. On the top of that you could use a similar (but not overlapping) universe (e.g. Canada vs US), different periods (1 week, 4 weeks, etc.), switching start date, or adding some noise by adding 10% of random stocks from a nonoverlapping universe. Then optimise your RS for each different training data set, and analyse variability in your parameters or use the same parameters and analyse variability in a performance metric.

Bias refers to the error that is introduced by approximating a real-life problem. In our case I would assume that the higher SR, Omega, the lower bias.

Ultimately, you would like to track how variance increases and bias decreases as you add new factors or degrees of freedom (more trees in random forest). For example, you would like to add a new factor to RS only if an increase in variance is suitably compensated by gain in bias (higher return).

19

From my experience, its possible to create very good systems using around 35 factors. Much more than that and the factors become too diluted, introducing too much noise. When I first joined P123 I had 100+ factor systems with sub 1% allocations for each factor… I was able to curve fit some amazing systems that performed terribly. Now my best out of sample performers use around 35 factors, which I would consider complex. I also think you need to use an external program to help you test systems with that many factors.

Tony

20

So we have few if any independent factors in our ranking systems. For example, FCF/P is not an “independent factor” if your system also has FCF/EV. EBITDA/EV is not fully independent if you use FCF/EV in your ranking system either. This is a collinearity problem.

There are automated solutions to this. Including recursive feature elimination which can be done in python with linear models, random forests, XGBoost etc…

For linear models LASSO regression can be used to eliminate factors as well as principle component analysis.

As a practical matter I do not know the ideal number. But I agree with Tony that around 35 factors can work with cross-validation and out of sample.

Many do use machine learning now and P123 will providing it. The number of factors I use is determined by the results of a time-series validation. My machine learning method is unique however (e.g., not linear regression, not a random forest not anything you would have heard of).

When available through P123, I think a random forest does pretty good and could be used with recursive feature elimination. That is pretty resource intensive.

Jim