“Incremental Variables and the Investment Opportunity Set” Eugene F. Fama and Kenneth R. French (2015)

[Jrinne]

All,

I just purchased “Your Complete Guide to Factor-Based Investing” for $9.95 (Kindle Version). It is probably well worth the money just to get Appendix G.

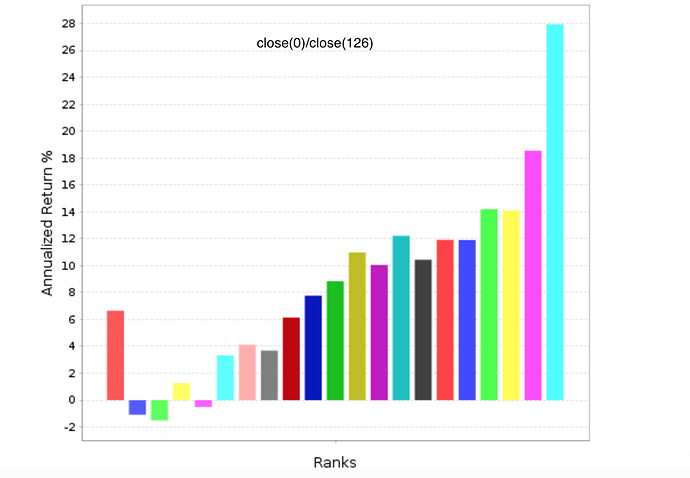
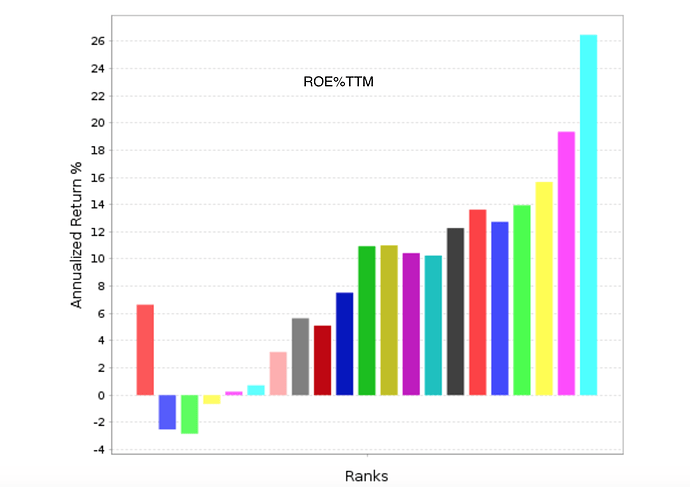
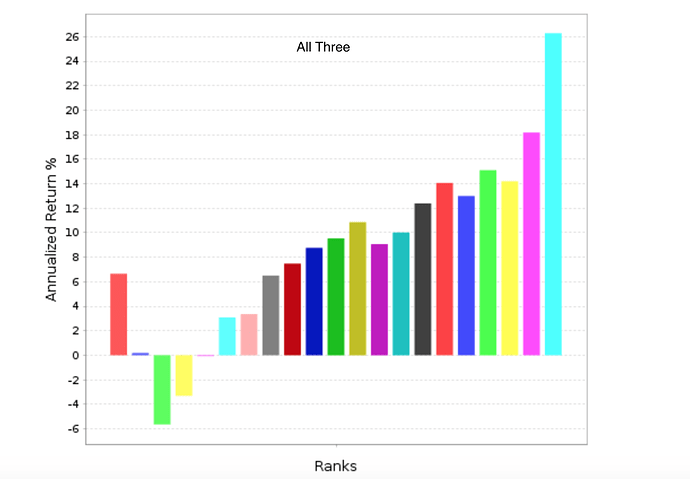
Appendix G is titled “Marginal Utility of Incremental Factors on Fund Returns” and discusses “Incremental Variables and the Investment Opportunity Set” Eugene F. Fama and Kenneth R. French (2015). In summary, this is a discussion of how many factors to use in a ranking system.

Because it is based on a recent paper by Fama and French it should probably be taken seriously. And I would have little to add (“I’m not worthy”: From the movie Wayne’s World).

But even if you disagree and you are in the more factors is better camp there is probably something you can use in this. For example, if you are adding a new factor to the ranking system does it matter whether the new factor has a positive correlation or a negative correlation to the factors that are already in your ranking system? If so, please explain (Oh sorry, I thought I was back in school for a second).

Or as they discuss in the appendix: How much does adding that new factor affect turnover and transaction costs? I do not mean to imply that the answer to this will be the same for everyone. Just that it is a good question.

Marc,
I leave to you to consider and express any opinion regarding Appendix G. But on my first read through the book I think it provides strong support for your ideas on the DDM and how the macroeconomy affects value stocks. Of course, they do not always come back to the DDM in this short book but I think you have said most or all of what the book says about this topic at some point. And there are some things—like the ability of small companies to get credit—that might not have been traced back to the DDM in your posts (I don’t recall).

Of course, I do not mean to imply that you agree with everything they say on this topic but is seem there is a lot of agreement on my first skim-through.

-Jim

[intvalueXXX]

Jim and All,

It may not be necessary to purchase the new Fama and French book to get access to the Appendix G information on what we would call ranking system factors. SSRN has several research papers by Fama and French titled,“Incremental Variables and the Investment Opportunity Set” that are publicly available for download in PDF format. The most recent one I see is from 2015:

[url=https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2509517]https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2509517[/url]

Perhaps Jim can compare the two versions and see if there are any updates/changes to the recent book and let us know? thanks

Chris

[Jrinne]

Christopher,

Thanks!. You are ahead of me. I meant to look up the origin paper. You made it easy and I will use your link. The book is by a different author and the appendix is just the author’s discussion of the topic/paper.

The appendix is good but nothing replaces the original paper.

I appreciate it!

-Jim

[yuvaltaylor]

Each additional factor you add will improve the overall quantile regression by less and less as you go. It couldn’t possibly be otherwise. I found the paper a little bit obvious, and I’m not sure what the takeaway is. It doesn’t seem like any other conclusions could have been possible.

I did my own experiment, and you can draw your own conclusions. I created an equally weighted ranking system with three factors, then added more factors to it until I had thirty equally weighted factors. At each step I did a performance measure on the Russell 3000 since 1999, rebalancing weekly. With thirty factors, they’re obviously not all uncorrelated.

My conclusion is that the more factors the better, but the increments are small. See attached.

---

incremental factors.pdf (728 KB)

[sgmd01]

Adjusted R squared is a better metric than R squared for a regression model as this metric will provide a penalty for a greater number of independent variables when R squared will not.

[intvalueXXX]

Yuval: "I created an equally weighted ranking system with three factors, then added more factors to it until I had thirty equally weighted factors. My conclusion is that the more factors the better, but the increments are small.

Yuval, There are many hundreds or thousands of possible factors and custom formula combinations in p123. So the result of your experiment, unless repeated with a random selection of factors to a degree of statistical significance, would entirely depend on which factors you added, right? I mean, I could create a Ranking System by selecting 30 factors that I know in combination would show a great return (because I have been working with p123’s tools for 13 years). Right afterward, I could select a different set of 30 factors and make the result show the opposite - that virtually every bar has negative returns.

One set of 30 factors could all be quality-related. The next 30 could be value-related. The next 30 could be technical factors. The number of possible permutations from combining hundreds or thousands of factors/custom formulas would be enormous. Now that I think of it, the number of permutations might even be infinite if you consider how many you could make from a simple factor such as “EMA(bars [,offset,series]).” That alone would be billions or trillions (or more?) of combinations using just EMA with all its possibilities. Then how about if you combined EMA several times in a formula, such as “EMA(20,2)>EMA(20,10) & EMA(100,2,$Series)>EMA(100,5,$Series).” Gazillions! haha

Maybe I don’t understand how you arrived at your conclusion, Yuval. To me, the result of your experiment would entirely depend on which factors you selected - unless it was randomly done in a controlled manner. Jim is a statistics guru; maybe he could tell us the number of random selections of factors we would have to create in order to produce a statistically significant factor-combination experiment to determine a range of ‘safe’ nodes to combine in a ranking system before it would begin to deteriorate from adding more factors.

Chris

[Jrinne]

thirty equally weighted factors.

30! (30 factorial) That is how many different orders that Yuval could have presented his findings (ordered his factors). 2.65 X 10^32 different ways. That is is lot of different ways.

So what I would like to see is the best combination of 7-9 factors and then add incremental factors from there.

But who can do that with any certainty? There are 2,035,800 ways to take 7 items out of 30. And if you also want to check if 8 or 9 factors are better starting point you have a little bit of work ahead of you. And remember, Yuval has made it easy on us by using equal weighting.

And I do not even know what factors Yuval is using.

But it gets worse. Fama and French (not Yuval) assume it is reasonable to use a linear model. Now look at Yuval’s rank performance graphs. Linear? I won’t even ask about multicollinearity, homoscedasticity, independence, etc.

This all gives me hope. I think it is hard to find a perfect solution using multivariate linear regressions. But if it were, D.E. Shaw would already be there.

More likely Yuval has found a thing or two that neither D.E Shaw or I know about (or could make a rational judgement about).

-Jim

[intvalueXXX]

We’re on the same page, Jim. This is why p123 members should never be concerned about sharing fairly detailed portfolio concepts in the forums. Someone else could be getting a completely different interpretation from my words, and the resulting stock-selections would be radically different. Unless you are actually sharing the character-by-character, digit-by-digit details of a Ranking System and Sim Buy/Sell rules, it’s unlikely any trade you get from a ’ proprietary’ system will ever be crowded in any one of our lifetimes.

So share away, folks! haha

Chris

[yuvaltaylor]

There are many hundreds or thousands of possible factors and custom formula combinations. So the results of your experiment, unless repeated with a random selection of factors to a degree of statistical significance, would entirely depend on which factors you added, right? I mean, I could create a Ranking System by selecting 30 factors that I know in combination would show a great return (because I have been working with p123’s tools for 13 years). Right afterwards, I could select a different 30 factors and make it show that virtually every bar has negative returns.

Maybe I don’t understand how you arrived at your conclusion, Yuval. To me, the result of your experiment would entirely depend on which factors you selected - unless it was randomly done in a controlled manner. Jim is a statistics guru; maybe he could tell us the number of random selections of factors we would have to create in order to produce a statistically significant factor-combination experiment to determine a range of ‘safe’ nodes recommended in a ranking system before it would begin to deteriorate from adding more factors.

Chris

Fama and French only tested factors that they knew worked. That’s what I did too. I was simply trying to replicate their experiment, and I don’t think my results are very different from theirs. The incremental increase by adding factors becomes extremely minor, but it’s still an increase (at least up to a point–there was no increase or benefit at all in going from 7 to 9 to 12 factors, and the difference between 25 and 30 factors is pretty marginal). Indeed, as you pointed out, I only used factors I knew worked well together. All I was trying to do was to show that if you use the right factors, more is better. Maybe Fama and French would agree, to a point.

On the other hand, if my experiment proves absolutely nothing, I apologize for bringing it up. I may have misunderstood what you two are getting at. Or what Fama and French are getting at, for that matter. I’m still kind of puzzled what their paper shows that isn’t pretty obvious if you think about it for ten minutes.

• Yuval

[Jrinne]

I may have misunderstood what you two are getting at. Or what Fama and French are getting at, for that matter. I’m still kind of puzzled what their paper shows that isn’t pretty obvious if you think about it for ten minutes.

The only criticism that I made was Fama and French’s assumption of linearity. While I am not willing to go as far as you in my criticism of them this sounds like it might be more a point of agreement than anything that would reflect on you.

I did describe the experiment that I would like to see but admitted that I did not want to go through 2,035,800 iterations (of just the starting ranking system). Not to mention the 21! or more ways that I could look at adding addition factors in a 30 factor ranking system. And I did not suggest that anyone else should (or could).

-Jim

[intvalueXXX]

Nor was I criticizing Yuval. I was only trying to discover what I had missed (which these days, seems to happen much more than I would like) from the logic of Yuval’s experiment.

I think that while there may be a nugget of wisdom in the Fama/French data, my guess is that we will each stick with what we believe works. If that means a Ranking System with 75 or more factors, then so be it. For myself, like Jim, I prefer to keep my number of variables in an RS to a minimum, as including more factors may have added a marginal amount to returns in the past, the more that is added the more it begins to feel like curve-fitting.

In the words of a very wise gentleman:

“A theory is the more impressive the greater the simplicity of its premises,
the more different kinds of things it relates, and the more extended its area of applicability.”

—Albert Einstein

[Jrinne]

I don’t think my results are very different from theirs [Fama and French].

It is pretty clear to me that Fama and French would not recommend using as many factors as Yuval or I use. There are clear differences in what Fama and French believe and what I do in practice. Perhaps, Yuval too.

But I reach a point of no improvement from adding additional factors much sooner than Yuval does–when I start with a certain set of core factors.

I won’t spend any more time trying to find out why that might be the case in this thread. But I do not believe this is a trivial discussion. IMHO, Fama and French are to be commended for their effort even if I believe some simplifying assumptions are required to make this complex subject tractable.

There was no attempt to criticize anyone else’s work. Indeed, I pointed out that there was no way to duplicate Yuval’s work–and have any judgement at all–due to the numbers involved and because I have no information regarding the factors used.

-Jim

[Miro]

Each additional factor you add will improve the overall quantile regression by less and less as you go. It couldn’t possibly be otherwise.

Sure it could. Depends on what factor you start with, and the order of additional factors.

[Jrinne]

Fama and French….I believe some simplifying assumptions are required to make this complex subject tractable.

My apologies to Fama and French.

My realization of my errors began with this in the paper: “Adding an explanatory variable can attenuate the slopes in a regression.” The truth of this is more evident if you are thinking of the slope of a line in multiple dimensions.

My problem was that I confused Rank Performance “slopes[sic]” with the real slopes of an n-dimensional line. Unless you have thought about the formula for the slope of a multidimensional line recently you might think there is some relation between the (apparent) magnitude of the two.

Forgetting this lead to other errors more directly related to my previous comments.

Maybe Fama and French did make a mistake or oversimplified. But looking for their mistakes is more likely to reveal my own errors and lead to a deeper understanding of the subject.

There is a reason they publish in peer-reviewed journals (and I don’t).

-Jim

[Miro]

My apologies to Fama and French.

No need to apologize. They’re human too.

First, Fama espoused the efficient markets hypothesis.

Then instead of admitting he was wrong, he published about exceptions to the rule, what he called “anomalies.”

He published about the size anomaly in 1994. Immediately afterwards, large caps crushed small caps from 1995-1999. Oops.

In 2007, he published that the size anomaly only works one way - a small company premium. Clearly, however, there is a big company penalty too (most of the time).

[DennyHalwes]

I would like to make 2 points about the value of properly selected additional factors. Yuval’s test example is a good one to show the 2 points.

First, there is a BIG difference in the differentiation of the 20 rank buckets between the 3 factor test and the 30 factor test.
The 3 through 9 factors exhibit some lower buckets have higher values then adjacent higher ranked buckets.
While the 15 through 30 factor tests show a smooth increase in performance from the lowest ranked buckets to the highest ranked.

Second, the 3 through 12 factor tests still show that the lowest bucket (not the S&P 500) has a positive return.
While the 15 through 30 factor tests show the lowest bucket has negative returns, with the 30 factor test having the most negative return.
Although the small increase in the max return of the highest bucket only increases slightly with more than 15 factors,
The 34 % range from the lowest bucket to the highest bucket is significantly greater for the 30 factor test than the tests with fewer factors.

These tests show that more factors, properly selected, can result in high probability of the finding stocks that, on average, will outperform most of the rest of the selected universe.

I have run the same basic tests for over a dozen years with a few additions. I always run the development of the ranking system with the rule EvenID = 1 in my universe to force the test to only look at 1/2 of the stocks in my universe. After I have developed a ranking system I feel meets my design plan using 20 buckets I test it using 50, 100, and 200 buckets. if the top bucket continues to have the highest performance, I repeat the tests with EvenID = 0 in my universe. This tests my ranking system on the other 1/2 of the stocks in my universe. If the performance of the new tests is similar to the original tests, I know that there is very little data mining or curve fitting in my new ranking system. I then rerun the test after removing EvenID = 0 from my universe and get the expected performance of the full universe.

[Jrinne]

So enough comments from the peanut gallery (meaning from me).

Yuval, at least, presented some results which is very much appreciated.

So kind of with my take. I took 5 core functions. Decided which ones ahead of time and did not change them. Equally weighted them and ran the rank performance test against the Prussell 2000.

I then added 3 factors to this. Pre-selected and ran just these three

1. Pr2SalesTTM
2. Close(0)/Close(126)
3. ROE%TTM

Then I ran it with all 3 added to the original core 5. Always equal weight.

My prediction ahead of time. Pr2SalesTTM would add a little but the others would make the performance worse.

My results below. Confusing label alert: All five means the initial 5 core functions. All three is all 3 additional factors added to the 5 core functions.

Did Pr2SalesTTM add a little bit? I think so but I had to get my reading glasses out.

My take: under certain conditions Fama and French might have a point. Specifically, when the original functions have high predictive value. But I have not proven this and I use the word “might” for good reason.

As always: There is a reason Fama and French publish in peer-reviewed journals (and I don’t). I’m just trying to contribute as all the previous posters did. All comments are very much appreciated.

Thank you.

My question for a long time: what causes the spike up for the last bucket? I think the shrinkage of the x-axis scale for Rank Performance compared to linear regressions is part. But interaction of variables, non-linearity to begin with and other things probably contribute.

-Jim

---

---

---

---

---

---

[mgerstein]

Marc,
I leave to you to consider and express any opinion regarding Appendix G. But on my first read through the book I think it provides strong support for your ideas on the DDM and how the macroeconomy affects value stocks. Of course, they do not always come back to the DDM in this short book but I think you have said most or all of what the book says about this topic at some point. And there are some things—like the ability of small companies to get credit—that might not have been traced back to the DDM in your posts (I don’t recall).

Of course, I do not mean to imply that you agree with everything they say on this topic but is seem there is a lot of agreement on my first skim-through.

-Jim

I’ll have to add it to my to-read list.

DDM aside, however, I worry about the sort of incremental analysis you describe them as doing. I worry that they are academic quants and nothing I’ve seen in their work suggests to me that either of them (or any of those who write based on their work) have ever done up close analysis of any specific companies. Unless one does that, and let’s one fingers walk slowly through lots of 10-Ks and 10-Qs, not to ,mention management conversations (conference calls nowadays), etc., it is easy for one to overestimate the conformity of the data and the ease with which a model can be “specified.”

For example, tests of incremental contribution, correlation, etc. to the contrary notwithstanding, I’m much more comfortable with a value model that uses five highly correlated factors rather than any one, even of the one can statistically be said to be the most informationally powerful. When we drill down from bucket analysis of large universes to manageable numbers of positions, it’s incredibly easy for a stock to be improperly classified because of a distortion in the data (not an error, but a distortion; i.e. Correct recording and computations based on numbers that don’t reflect underlying trends – in academia, exceptions are exceptions, in real life, especially in business, exceptions are the norm).And even without distortion, what makes for reasonable P/E, P/B, P/S ratios etc. are all driven by different company characteristics. It is often useful to take account of whether all the oars are in the after together or not.

We can never be 100% free from unintended specification errors. But the effort we make is what increases the probability that a well conceived model will give live performance in line with reasonable expectations.If I’m using five valuation metrics, even if two are distorted, there’s at least a tolerable change that three good ones can give me enough usable information to allow a model to functional at an acceptable level.

Put another way, when I think of the singular value factor I use, it’s the rank computed by the Basic: Value ranking system, or some other value ranking system; not the P/E, the P/S or any component of the system. (That’s why many screening/buy rules I use are based on the Rating() function.) The only time I use a single factor or formula is if I have a very high degree of confidence in the cleanliness of the company-specific specification, such as market cap as a proxy for size – but I may even re-think that after we complete the formula weighting and I gain more experience with smart beta.

[davidbv]

Just as a general comment, it is interesting that in portfolio construction you want to use less correlated assets (to improve return and decrease Standard Deviation of the whole portfolio) while in model construction one wants more correlated rules that are co-reinforcing to each other. I am still wrapping my mind around that one.

[Jrinne]

……use less correlated assets (to improve return and decrease Standard Deviation of the whole portfolio) ….

David,
The book I recommended says this very same thing. In addition, when one does not focus too much on one appendix (as I have done), the author suggest using a number of diversifying factors to reduce risk. Which presumably means increasing the number of factors.

Good point!

-Jim