Yes, kitchen sink is always the best or at least the second best
You can beat the SP500, but it's not worth it. Because you don't have a sophisticated trading system, cheap leverage and a low-cost source of stock borrowing.The SP500 and even the Russell 1000 are the domain for billionaires, not retail stock pickers.
Well I feel like I seen many large cap systems on here with 10-20 stocks for long periods that can outperform Sp500 based on some ranking system like Core Combination with 3-5 buy/sell rules combined.
I said
"You can beat the SP500, but it's not worth it"
Perhaps relevant
We introduce artificial intelligence pricing theory (AIPT). In contrast with the APT’s foundational assumption of a low dimensional factor structure in returns, the AIPT conjectures that returns are driven by a large number of factors. We first verify this conjecture empirically and show that nonlinear models with an exorbitant number of factors (many more than the number of training observations or base assets) are far more successful in describing the out-of-sample behavior of asset returns than simpler standard models. We then theoretically characterize the behavior of large factor pricing models, from which we show that the AIPT’s “many factors” conjecture faithfully explains our empirical findings, while the APT’s “few factors” conjecture is contradicted by the data.
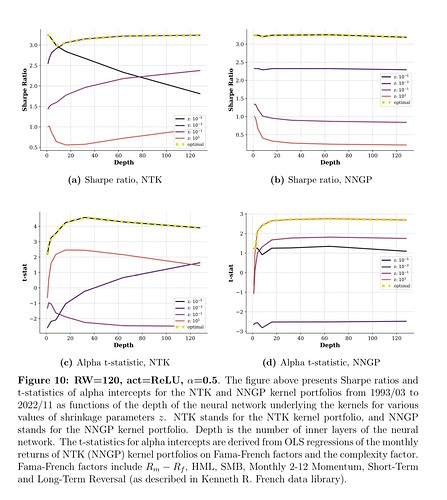
"The largest model we consider (with 360,000 factors ..." ![]()
Yes. But generated from 130 factors by a neural-net. Then put into a model using ridge regression. Non-linear they say so I guess they mean L2 regularization.
Still 130 may be a lot and I am not really commenting on the number we should use here at P123 with our models at this point..
But if you are going to go through all that is it different than just plugging 130 factors into a deep neural-net?
A neural-net will effectively create additional factors (from the original 130) within its layers, I am thinking. Maybe not so different than what we would think of as plugging 130 factors into a neural-net, if I understand. Maybe I don't (understand) BTW.
One could also create new interaction-variables in linear models if you want more factors in your linear models.
They are not the same. The authors have tried wide and deep neural networks. Their results are not as good.
https://arxiv.org/pdf/2402.06635
The best result is from the simplest one-layer NN and worse than the ridge models.
This result is exactly what I said: the optimal strategy in large-cap stocks is linear models. They are even simpler than DNNs.
The problem with sparse models is that they underestimate model uncertainty too much.
Complexity is really only used to reduce the impact of model uncertainty as the usual double descent phenomenon. The "signal to noise" and "solution space" paradigms impose excessive constraints on machine learning now.
This means that searching for hundreds of thousands of kinds of weights and then combining them in some way pays off. But given the computational complexity of the ridge algorithm, I don't think those efforts are really cost-efficient for most people here. I would recommend it to large asset management companies and the ultra-rich though.
Here's a different take; https://www.portfolio123.com/app/r2g/summary?id=1420190 uses 5 factors and works well against the S&P500 dividend universe. Two of the factors are dividend yield based.
No kitchen sink needed.
Has anyone tried interactive variables for their linear models? That seems like it has potential and adds new variables that may have new information. It would be practical for almost every P123 user. It could even be tried in P123 classic.
I am serious that interactive variables should be looked at, I have tried it. but my experience is limit for now.
With just 9 factors one can increase the total number of factors to 363,800 beating the researchers in the paper (i.e., 9!) if you check every interaction. I am sure the paper has a better way. But, anyone can create interactive variables at P123.
And more than a few members like linear models (where one uses interactive variables). Seems like a method that could be explored for adding new factors.
You can also use a ridge regression or "ridge regularization" as the authors do in their paper. All within P123's AIFactor offering.
Claude 3 had this to add to the discussion of interactive variables: "It offers a way to introduce non-linearity"
Linear models have been the most successful for me. I can add that much. Scraping old ranking systems and running the (interactive?) factors through linear lasso yields some interesting results. One of these days I'll dig in the model holdings to better understand why it works so well. Attached is the result of a ranking system using a linear lasso based AIFactor() against several universes.
What do you mean by "interactive variables"?
TL;DR: Linear methods including ridge regression do not account for interaction of the variables.
An interaction term is the product of 2 variables. So for example (EV to Sales) * (Surprise%Q1). Generally the model includes the original terms also.
You would accomplish much of what the paper is doing by adding interaction variables (also called interaction features) to a ridge regression in P123's AI/ML is my point. Arguably achieving most of what is being accomplished in the paper and it is practical.
I leave it to people's domain knowledge to determine which features to try this with in the real world. But if you tested every interaction for 130 features (130 features in the paper) you could generate 1.3 x 10^218 interactive features (130! or 130 factorial).
So with regard to the paper I am not sure why they stopped at 363,800 features. Would they be able to use their domain knowledge on the neural-net created factors?
Early in the morning I think Claude 3 summarizes the potential advantages better than my first attempt:
-
Literal Interpretation:
- Interaction variables capture how two or more factors "interact" or influence each other's effects on the outcome variable.
- This is not just a statistical construct, but often reflects real-world phenomena.
-
Real-World Example from Stock Investing:
- Factor A: Price-to-Earnings Ratio (P/E)
- Factor B: Interest Rates
-
Individual Effects:
- Each factor might affect stock returns independently.
-
Interaction Effect:
- The interaction between P/E and interest rates could be crucial:
- When interest rates are low:
- Investors might be more willing to pay higher P/E ratios for growth stocks.
- When interest rates are high:
- Lower P/E stocks might be more attractive.
- When interest rates are low:
- The interaction between P/E and interest rates could be crucial:
Anyway, this is at least practical for P123 members to try relative to the paper's method. And it could be a productive place to look for new factors. Especially for those using linear models.
Jim
The Fed model is wrong, and the vast majority of people don't actually rely on the discounting model for trading.
This has the appearance but not the reality of common sense. The empirical evidence tells us the Fed model has no power to forecast long-term real stock returns. On the contrary: Traditional methods, like examining the market’s unadjusted P/E alone, have been very effective.
In the end, we believe the Fed model is a misleading sales tool for stocks. Its popularity is presumably driven by its simplicity; its flexibility (if you don’t like the E/P, just call some expenses non-recurring); its superficial rigor (it looks like math); its false initial resemblance to common sense (pundit after pundit enjoys explaining to a presumably impressed audience how bonds really have a P/E too); and most assuredly the fact that it is now, and for some time has been, more bullish than the traditional model.
But (real) interest rates may affect leverage-related factors because companies actually have to pay interests.
For common variables seen in the core ranking system (i.e., not a secret) I wonder it we might want to get a forum thread where people share interactive variables that members find useful. I have started on the 1.3 x 10^218 possibilities and am already tired. ![]()
Assuming this is something that members find useful.
Correction: the number of possible 2 way interaction for 130 variables is actually "130 take 2" NOT 130 factorial. That calculates out to only 8,385 two-way interactions.
I think it's best to have a place where all useful features/methods are shared.
A new paper shows that the everything-but-the-kitchen-sink approach is empirically better than using a limited number of factors: https://www.nber.org/papers/w33012#fromrss
The abundance of anomalies (the so-called “factor zoo”) is not a puzzle to be solved or evidence of a corrupt research process.3 Instead, it is the theoretically expected outcome in a complex asset pricing environment because data limitations hamper our ability to learn the true nature of markets. In fact, our theory argues that the extant factor zoo is too small and that an SDF model can be beneficially expanded to incorporate a teeming Noah’s ark of factors by transforming raw asset characteristics into a wide variety of nonlinear signals (buttressed by appropriate shrinkage). Such a large factor set improves the out-of-sample SDF Sharpe ratio and reduces out-of-sample pricing errors.
(SDF stands for stochastic discount factor.)
How many factors in the way that we think of factors did the writers of this paper find useful? Is it 130 perhaps?
"The information set includes 130 well-known characteristics for the cross-section of US stocks. To vary the number of pricing factors, we use a neural network to generate new stock characteristics—up to hundreds of thousands—that are nonlinear transformations of the original 130 variables."
130 is not a small number for sure. But 130 would be my count for P123-classic-type factors used in this paper.
Using P123's non-linear AI/ML models will also create new factors for you--in the sense that the paper means. There is no doubt that this can be useful, I believe. But it is not factors like we normally think of here at P123.
To be clear, I have been a strong advocate for adding non-linear models (that naturally generate new factors in the sense that the paper means). Something Marco has already done. In that sense the paper has a good point.
ChatGPT check for accuracy: "Your point about the distinction between traditional factors and machine-learning-generated ones is clear and highlights an important difference in how factors are discussed in different modeling contexts."
Jim